√99以上 construct the graph x^2 y^2=9 116581

Identify the shape of z = 9 y^2, x^2 y^2 = 5, z = 4 x, and 9x^2 7y^2 z = 0 Create an account to start this course today Used by over 30 million students worldwideColumn "B", list your data that will be placed on the "y" axis of the graph 2 Using your mouse, highlight the data 3 Go to the "Insert" menu, and select "Scatter" 4 Choose the first box (no lines) 5 Using the "Chart Tools" menu, title your graph and label the x and y axis, with correct units 6 Click the chart areaFind the vertex and focus of y2 6y 12x – 15 = 0 The y part is squared, so this is a sideways parabola I'll get the y stuff by itself on one side of the equation, and then complete the square to convert this to conics form y2 6 y – 15 = –12 x y2 6 y 9 – 15 = –12 x 9 (

Find Points On The Curve X 2 9 Y 2 16 1 At Which The Tangents Are I Parallel To X Axis Youtube

Construct the graph x^2 y^2=9

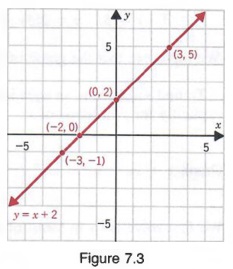
Construct the graph x^2 y^2=9-9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 f 0 (x) f 8 (x) f 1 (x) (x 5,y 5) (x 6,y 6) y x In this example, the ten control points have ascending values for the xcoordinate, and are numbered with indices 0 through 9 Between each control point pair is a function, which is numbered identically to the index of its leftmost point In general, f i(x) = a iIf we graph the points determined by these ordered pairs and pass a straight line through them, we obtain the graph of all solutions of y = x 2, as shown in Figure 73 That is, every solution of y = x 2 lies on the line, and every point on the line is a solution of y = x 2

How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic

And the area of R is given by A R E A = ∫ c d w ( y) d y = ∫ c d ( r ( y) − l ( y)) d y EXAMPLE 2 Compute the area of the region in the plane enclosed by the graphs of y = 2 x and y = x 2 Using vertical crosssections we have that 0 ≤ x ≤ 2 a n d x 2 ≤ y ≤ 2 x so that the area of the region isGraph f(x) = −2x 2 3x – 3 a = −2, so the graph will open down and be thinner than f(x) = x 2 c = −3, so it will move to intercept the yaxis at (0, −3) Before making a table of values, look at the values of a and c to get a general idea of what the graph should look likePrecalculus Geometry of an Ellipse Graphing Ellipses 1 Answer MrsRudolph221 This is the standard form for the graph of a circle!

It will plot functions given in the form y = f(x), such as y = x 2 or y = 3x 1, as well as relations of the form f(x,y) = g(x,y), such as x 2 y 2 = 4 To use the plot command, simply go to the basic plot page , type in your equation (in terms of x and y), enter the set of x and y values for which the plot should be made and hit the Plot14 Direction Fields 41 2 The isocline method might also be used to select grid points For details on both methods, see the next subsection 3 The arrow shaft is a replacement curve for the solution of y0 = f(x,y) through grid point (x∗,y∗) on a small xinterval, called a lineal elementCircle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples x y x 2 y 2;

To graph an ellipse, visit the ellipse graphing calculator (choose the Implicit option) Enter the information you have and skip unknown values Enter the equation of an ellipse In any form you want `x^24y^2=1`, `x^2/9y^2/16=1`, etc Enter the center ( , ) Enter the first focus ( , ) Enter the second focusSafety How works Test new features Press Copyright Contact us Creators5 0 5 2 0 2 = 25 0 = 25 3 4 3 2 4 2 = 9 16 = 25 0 5 0

A Graph For The 3 27 3 2 1 2 9 Code Two Z3weighted Star Download Scientific Diagram

Ellipses And Hyperbolae

Erdem is going to construct a rectangular paper box he will make the box x inches wide the length of the box will be 2 inches more than its width, and the411 Recognize a function of two variables and identify its domain and range 412 Sketch a graph of a function of two variables 413 Sketch several traces or level curves of a function of two variables 414 Recognize a function of three or more variables and identify its level surfaces Our first step is to explain what a function ofNow with axes labelled and a plot label Plot x, x^2, x^3, x^4 , x, 1, 1 , AxesLabel x, y , PlotLabel Graph of powers of x 10 05 05 10 x1005 05 10 y Graph of powers of x Notice that text is put within quotes Or to really jazz it up (this is an example on the Mathemat

Graphing Square Root Functions

Intercepts Of Lines Review X Intercepts And Y Intercepts Article Khan Academy

F( x ) = √ (x 2 9) Solution to Example 5 The domain of the function given above is found by solving x 2 9 ≥ 0 Which gives a domain reprsented by (∞ , 3 U 3 , ∞) We now select values of x in the domain of f to construct a table of values, noting f(x) = f(x) hence a symmetry of the graph with respect to the y axisThe last equation graphs a parabola How To Graph a Circle Equation A circle can be thought of as a graphed line thatSince, as we just wrote, every linear equation is a relationship of x and y values, we can create a table of values for any line These are just the $$ x $$ and $$ y $$ values that are true for the given line In other words, a table of values is simply some of the points that are on the line

How To Construct The Graph Of X 2 Y 2 9 Quora

Graphing Square Root Functions

First remember that solutions to the system must be somewhere on the graph of the constraint, \({x^2} {y^2} = 1\) in this case Because we are looking for the minimum/maximum value of \(f\left( {x,y} \right)\) this, in turn, means that the location of the minimum/maximum value of \(f\left( {x,y} \right)\), ie the point \(\left( {x,y} \right)\), must occur where the graph ofGraph x^2y^2=9 x2 y2 = 9 x 2 y 2 = 9 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the412 Quadratic Interpolation Assume three data points (x 0,y 0),(x 1,y 1),(x 2,y 2), with x 0,x 1,x 2 distinct We construct the quadratic polynomial passing through these points using

Graph Using Intercepts

Please Help Urgent Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25 Brainly Com

Sin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean =0 It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsK then y righty 5 else y lefty 6 return (\NOT FOUND) 8Graph the parametric equations x = 5 cos t \displaystyle x=5\cos t x = 5 c o s t and y = 2 sin t \displaystyle y=2\sin t y = 2 s i n t First, construct the graph using data points generated from the parametric form Then graph the rectangular form of the equation

Graph Graph Equations With Step By Step Math Problem Solver

How To Construct The Graph Of X 2 Y 2 9 Quora

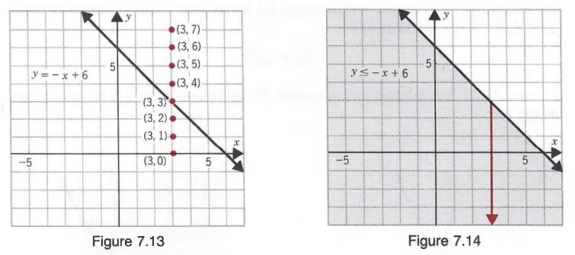
Answer (1 of 3) It's the equation of sphere The general equation of sphere looks like (xx_0)^2(yy_0)^2(zz_0)^2=a^2 Where (x_0,y_0,z_0) is the centre of the circle and a is the radious of the circle It's graph looks like Credits This 3D Graph is created @ code graphing calculatorNow we may construct the graph of this equation as below Solution 2 We may observe that point (2, 14) satisfies the equation 7x y = 0 and 2x y 18 = 0 So, 7x y = 0 and 2x y 18 = 0 are two lines passing through point (2, 14) The graph of equation x y = 100 can be drawn as followsThe fourth equation is the familiar slopeintercept form;

Rectangular Coordinate System

How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic

Y = x 2 6 x 3;This example illustrates how the b and m terms in an equation for a straight line determine the position of the line on a graph As noted above, the b term is the yinterceptThe reason is that if x = 0, the b term will reveal where the line intercepts, or crosses, the yaxisIn this example, the line hits the vertical axis at 9 The m term in the equation for the line is the slopeAnswer (1 of 11) There's a simple answer, if you don't wish to think — you can find it in all the other answers given But I'll assume you'd like to understand what's happening here I tutor fifth and sixthgrade students and this is exactly how I'd describe it to them The graph of x^2 y^2

Graphing A Linear Equation Y 2x 7 Video Khan Academy

Example 13 Define Function Y F X X 2 Complete The Table

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &In a graph Traversal strategies can be speci ed by the ordering of the three objects to visit the current node, the left subtree, y x 2 while y 6= nil do 3 if keyy=k then return y 4 else if keyy<Create a graph of y=2x−6 Construct a graph corresponding to the linear equation y=2x−6 PlainMath SECONDARY ALGEBRA ALGEBRA I LINEAR EQUATIONS AND GRAPHS Secondary Calculus and Analysis

How To Construct The Graph Of X 2 Y 2 9 Quora

Graph Graph Equations With Step By Step Math Problem Solver

Steps to graph x^2 y^2 = 4Analyzing the Graphs of y = sec x and y = cscx The secant was defined by the reciprocal identity sec x = 1 cos x sec x = 1 cos x Notice that the function is undefined when the cosine is 0, leading to vertical asymptotes at π 2, π 2, 3 π 2, 3 π 2, etc Because the cosine is never more than 1 in absolute value, the secant, being the reciprocal, will never be less than 1 in absolute valueConstructing Basic Blocks Assume that the input is a list of tuples How do we ¯nd the beginning and end of each basic block?

Sketch The Graph Of The Set X Y X2 Y2 9 Wyzant Ask An Expert

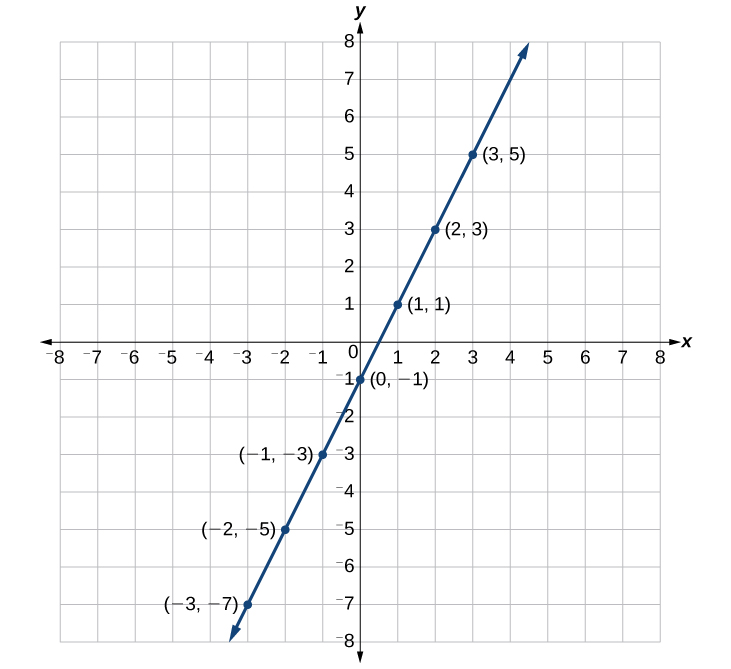
The Rectangular Coordinate Systems And Graphs Algebra And Trigonometry

Y 2 (x) = g(2/3x) = cos (2/3x), construct a table of values, and plot the graph of the new function As you can see, the graph of y 2 ( x ) is in fact the base graph g ( x )X 4 2 y 6 2 = 49;Graph 3x^2y^2=9 Find the standard form of the ellipse Tap for more steps Divide each term by to make the right side equal to one Simplify each term in the equation in order to set the right side equal to The standard form of an ellipse or hyperbola requires the right side of the equation be

Implicit Differentiation

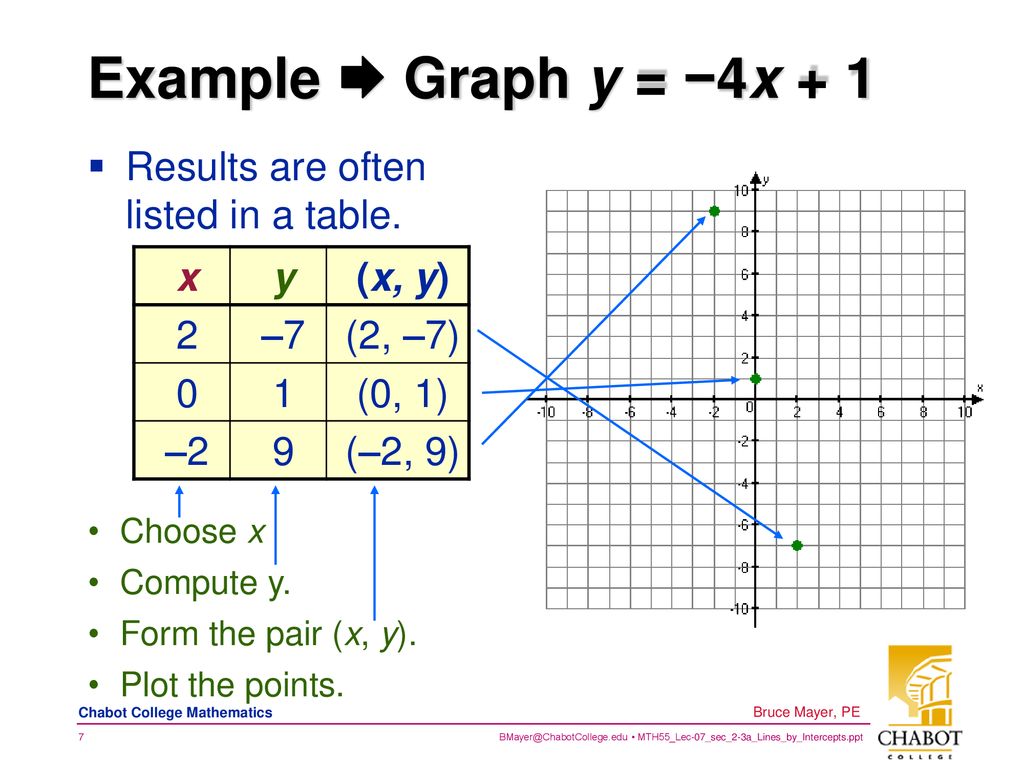
Licensed Electrical Mechanical Engineer Ppt Download

Example 1 Sketch the parametric curve for the following set of parametric equations x = t2 t y =2t−1 x = t 2 t y = 2 t − 1 Show Solution At this point our only option for sketching a parametric curve is to pick values of t t, plug them into theX 5 2 y 9 2 = 81;(Section 13 Basic Graphs and Symmetry) 134 TIP 1 The graph never falls below the xaxis, because squares of real numbers are never negative Look at the table Each pair of opposite x values yields a common function value fx(), or y • Graphically, this means that every point ()x, y on the graph has a "mirror image partner" () x, y that is also on the graph

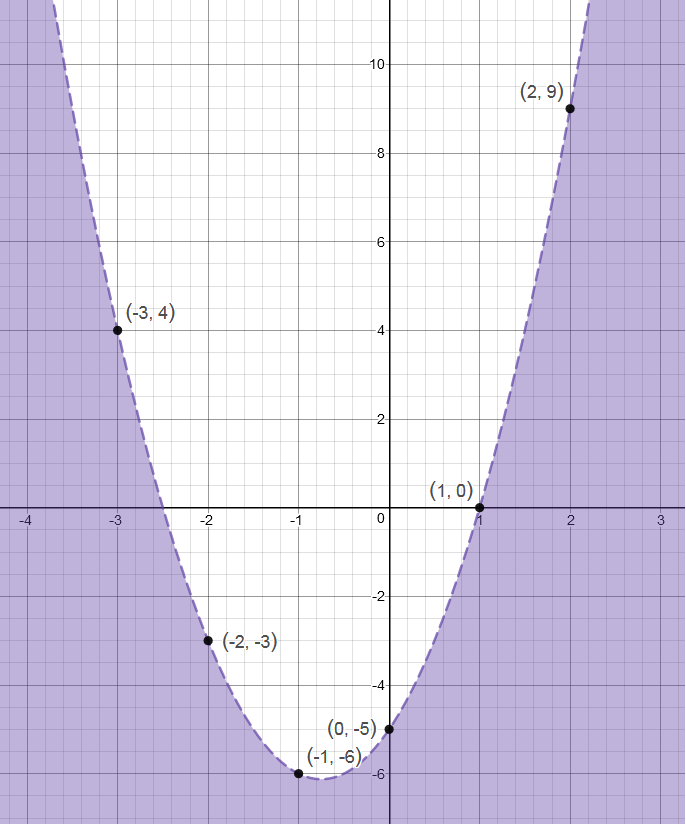
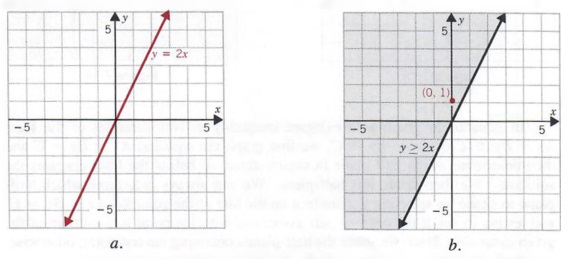
How Do You Graph The Inequality Y 2x 2 3x 5 Socratic

Biomath Transformation Of Graphs

2 If the graph touches the xaxis and bounces o↵the axis, it is a zero with 3 The sum of the multiplicities is to construct the lowestdegree polynomial Example 11 Construct the lowestdegree polynomial given the zeros below 3,3,4 14 X K X_9 IS A ZERO OFTHE FUNCTION f 2 11 9 IS A SOLUTION OFTHE EQUATION f1 3 02 g(x) = 2 3 x 1 3 h(x) = 2x2 1 x2 1 3x 2 x2 1 4 r(x) = 2x2 1 x2 1 3x 2 x2 1 Solution 1To nd the domain of f, we proceed as we did in Section14 we nd the zeros of the denominator and exclude them from the domain Setting x1 = 0 results in x= 1 Hence,SOLUTION 1 Let variables x and y represent two nonnegative numbers The sum of the two numbers is given to be 9 = x y, so that y = 9 x We wish to MAXIMIZE the PRODUCT P = x y 2 However, before we differentiate the righthand side, we will write it as a function of x only Substitute for y getting P = x y 2 = x ( 9x) 2 Now differentiate this equation using the product

How Do You Graph X 2 Y 2 4 Socratic

How Do You Graph X 3 2 Y 5 2 16 Example

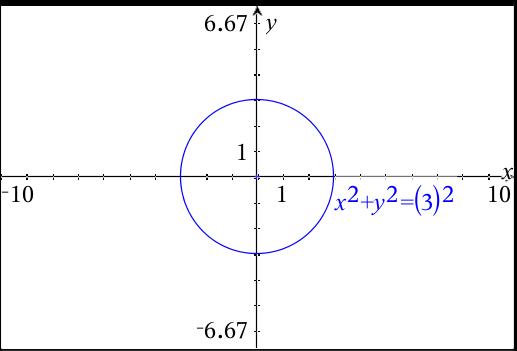
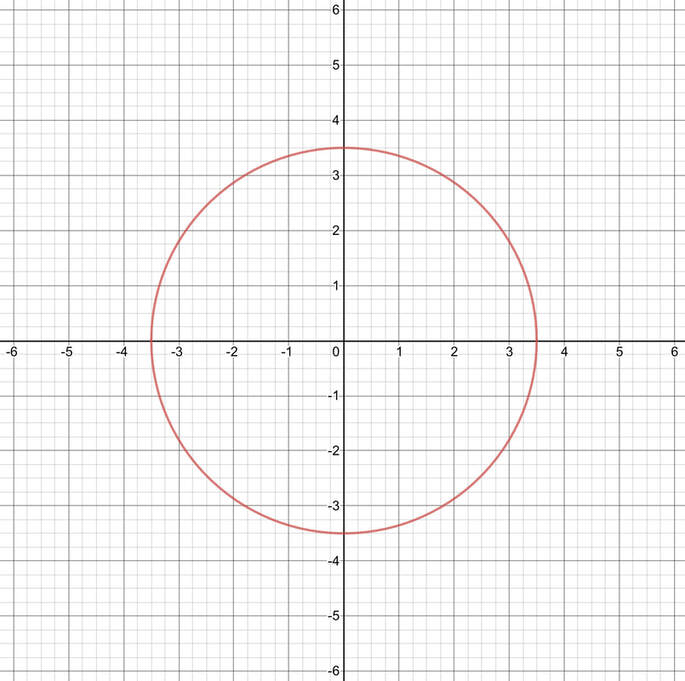
Similarly, the graph of y = x 2 3 is 3 units below the graph of y = x 2 The constant term c has the same effect for any value of a and b Parabolas in the vertexform or the ahk form, y = a(x h) 2 k To understand the vertexform of the quadratic equation, let's go back our orginal equation, f(x) = x 2 In this equation, rememberStep 2 Determine a Scale Start with the horizontal scale If you are using graph paper, let 1 unit on the graph paper equal 1 unit of the values you are graphing Determine whether the greatest value will fit on the graph If it doesn't, then change the scale and try again Now repeat this process for the vertical scaleThe graph of x^2y^2=9 represents a graph of a circle On the given graph you can also find all of the important points for function x^2y^2=9 (if they exist)

X 2 Y 2 9 Find A Polar Equation For The Curve Represented By The Given Cartesian Equation Youtube

Writing Exponential Functions From Graphs Algebra Video Khan Academy

#(xh)^2(yk)^2=r^2# Doesn't a circleCS 412/413 Spring 08 Introduction to Compilers 1 CS412/CS413 Introduction to Compilers Tim Teitelbaum Lecture 24 Control Flow Graphs 24 Mar 08Graphs of Logarithm Functions (Sect 43) – Tutorial Worksheet (a) Follow the instructions to construct the graph of f (x) = log 2 x Recall, f (x) = log 2 x means y = log 2 x The exponential form of y = log 2 x is 2 y = x So, we find (x, y) values to plot y

Graph Graph Equations With Step By Step Math Problem Solver

Solve Ellipse And Hyperbola Step By Step Math Problem Solver

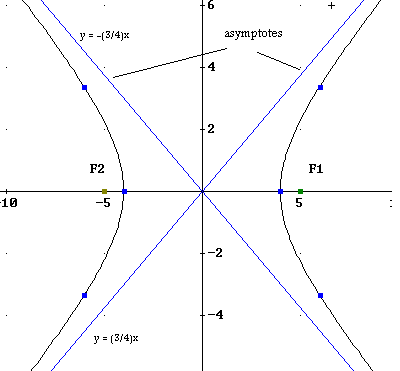
A quick guide to sketching phase planes Section 61 of the text discusses equilibrium points and analysis of the phase plane However, there is one idea, not mentioned in the book, that is very useful to sketching and analyzing phaseThe difference between the two forms is the interchange of (xh) and (yk) y^2x^2=9 y^2/9x^2/9=1 Given equation is a hyperbola with center at (0, 0) and it has a vertical transverse axis a^2=9 a=3 2a=6=transverse axis vertices (0,0±3) b^2=9 b=3 2b=6=conjugate axis Equation of asymptotes y=±(a/b)x See the graph below as a visual checkNow let's graph more values of n between 2 and 3 to see the changes in the graphs As you can see from this graph, as the parameter n gets larger and larger, the graph transforms more and more from an ellipse to a hyperbola Next, let's observe the graph of the equation x 2 3xy y 2 = 9 You can see that this appears to be a graph of a hyperbola oriented around the origin with x

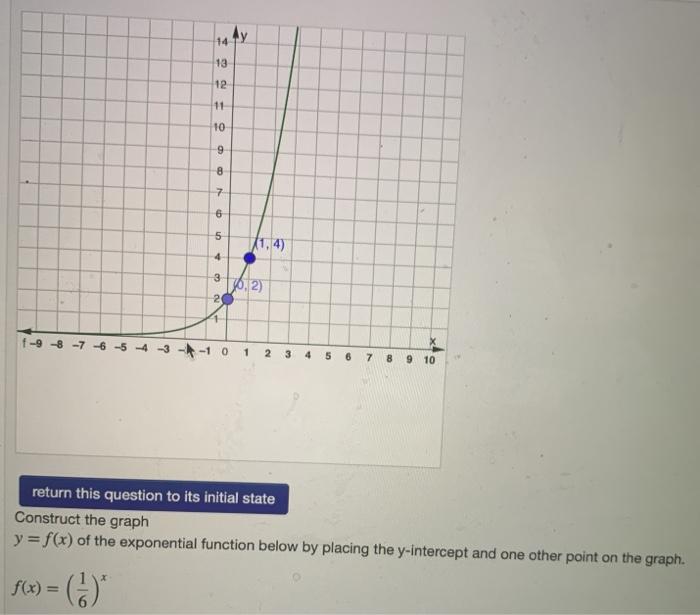
Solved 1 Point Construct The Graph Y F X Of The Chegg Com

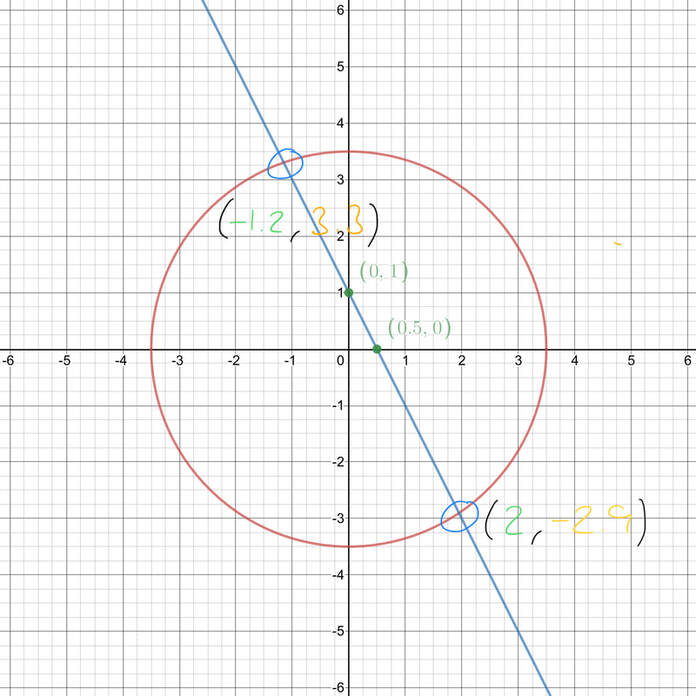
A Graph Of X 2 Y 2 9 Is Shown On The Grid By Drawing The Line X Y 2 Solve The Equations X 2 Brainly Com

A value larger than 1, smaller than 1 but greater than 0, and less than 0 They are then asked to compare the tables and graphs for y = x 2, y = 2 * x 2, y = 3 * x 2, y = 4 * x 2, etc and to describe in words what patterns they find Finally, students are asked to compare the table of values for y = 2 * x 2 and y = 2 * x 2 and describe whatHow do you graph #x^2y^2=9# and what are its lines of symmetry?Only equations 1, 3, 5 and 6 are centerradius forms The second equation graphs a straight line;

A Graph Of X 2 Y 2 9 Is Shown On The Grid By Drawing The Line X Y 2 Solve The Equations X 2 Brainly Com

Graph Of An Equation

1 First determine a set of leaders , the ¯rst tuple of basic blocks 1 The ¯rst tuple is a leader 2 Tuple L is a leader if there is a tuple if goto L or goto L 3 Tuple L is a leader if it immediately follows a tuple if goto B or goto B

Q16 Answers Paper 2 June 18 Edexcel Gcse Maths Higher Elevise

Graphing A Circle Help Mathskey Com

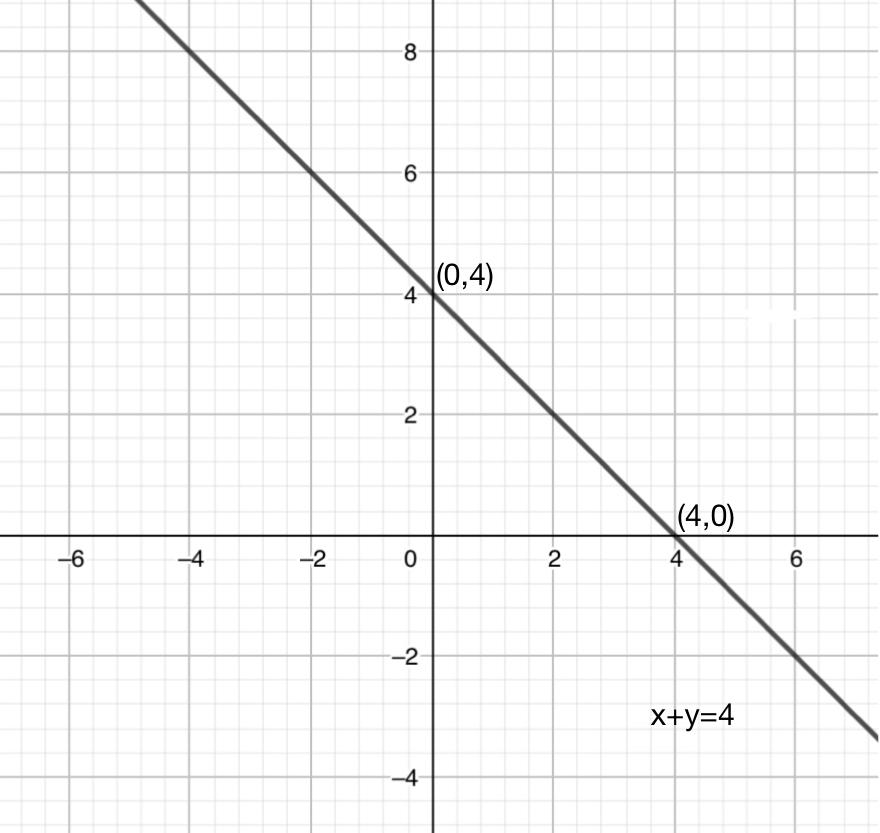
Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse

Graph Y X 7 X 3 Mathskey Com

Graphing Parabolas

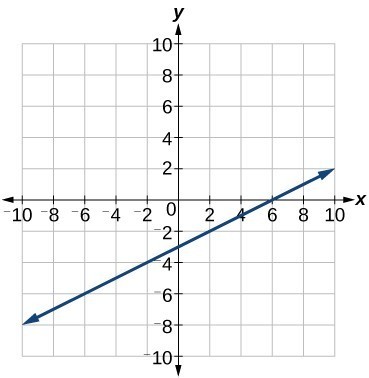
Write The Equation For A Linear Function From The Graph Of A Line College Algebra

12 6 Quadric Surfaces Mathematics Libretexts

13 E Vector Valued Functions Exercises Mathematics Libretexts

Surfaces Part 2

Scarpelli Assignment 2

How To Graph A Circle 4 Easy Steps Equations Examples Video

Solution Find The X And Y Intercepts Of Each Graph Y X 2 9

Pplato Basic Mathematics Quadratic Functions And Their Graphs

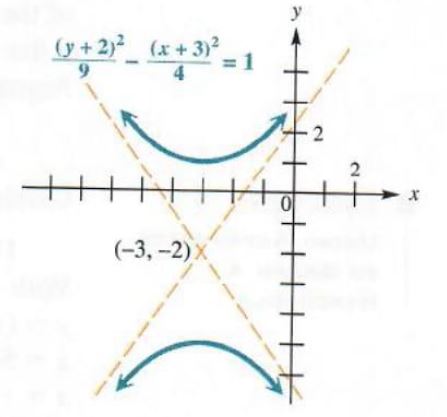
Solution Find The Vertices And Foci Of The Hyperbola Draw The Graph Y 2 25 X 2 21 1 X 2 9 Y 2 16 1

Pplato Basic Mathematics Quadratic Functions And Their Graphs

Pplato Basic Mathematics Quadratic Functions And Their Graphs

How To Graph A Circle 4 Easy Steps Equations Examples Video

How To Construct The Graph Of X 2 Y 2 9 Quora

14 1 Functions Of Several Variables Mathematics Libretexts

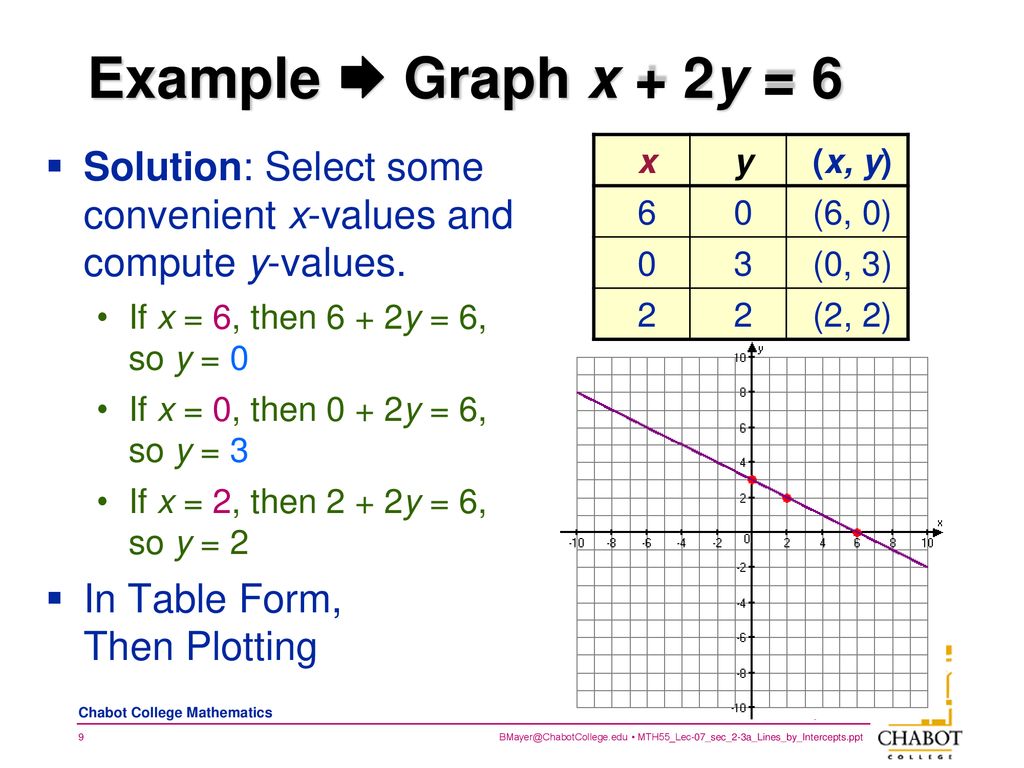
Licensed Electrical Mechanical Engineer Ppt Download

100以上 Yx2 ニスヌーピー 壁紙

Sketch The Graph Of The Set X Y X2 Y2 9 Wyzant Ask An Expert

Scarpelli Assignment 2

Graphing Square Root Functions

Graphing Parabolas

Construct The Graph Of X 2 Y 2 9 What Would This Graph Look Like And What Are Its Coordinates Please Brainly Com

1

Elipse Geogebra

Find Points On The Curve X 2 9 Y 2 16 1 At Which The Tangents Are I Parallel To X Axis Youtube

Equation Of A Circle

Scarpelli Assignment 2

Graph Plotting In Python Set 1 Geeksforgeeks

How To Construct The Graph Of X 2 Y 2 9 Quora

How To Construct The Graph Of X 2 Y 2 9 Quora

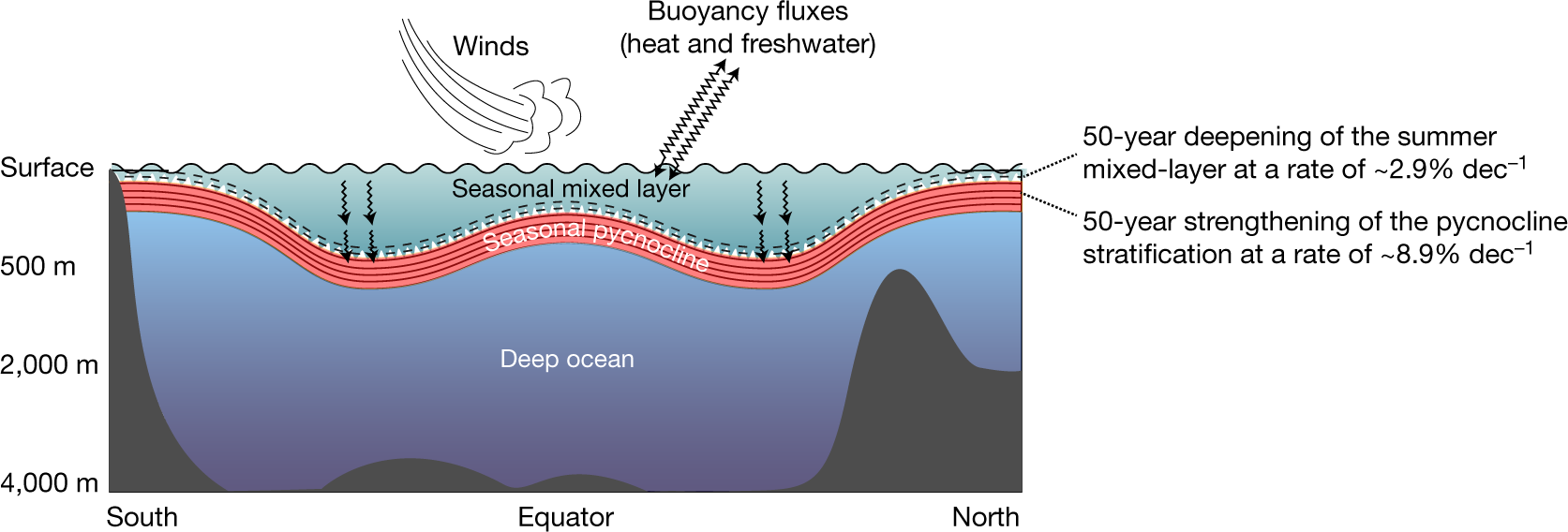
Summertime Increases In Upper Ocean Stratification And Mixed Layer Depth Nature

12 6 Quadric Surfaces Mathematics Libretexts

Q16 Answers Paper 2 June 18 Edexcel Gcse Maths Higher Elevise

Graph By Plotting Points

1

最も選択された Y X2 2 Graph ニスヌーピー 壁紙

Does X2 Y2 9 Represent Y As A Function Of X Youtube

Graphing Quadratic Functions

Q16 Answers Paper 2 June 18 Edexcel Gcse Maths Higher Elevise

Scarpelli Assignment 2

How To Graph X 2y 6 Quora

For The Circle With Equation X 2 2 Y 3 2 9 Find The Following A What Are The Coordinates Of The Center B What Are The Radius And Diameter Of

Quadratic Function

Quadratic Function

How To Construct The Graph Of X 2 Y 2 9 Quora

How To Construct The Graph Of X 2 Y 2 9 Quora

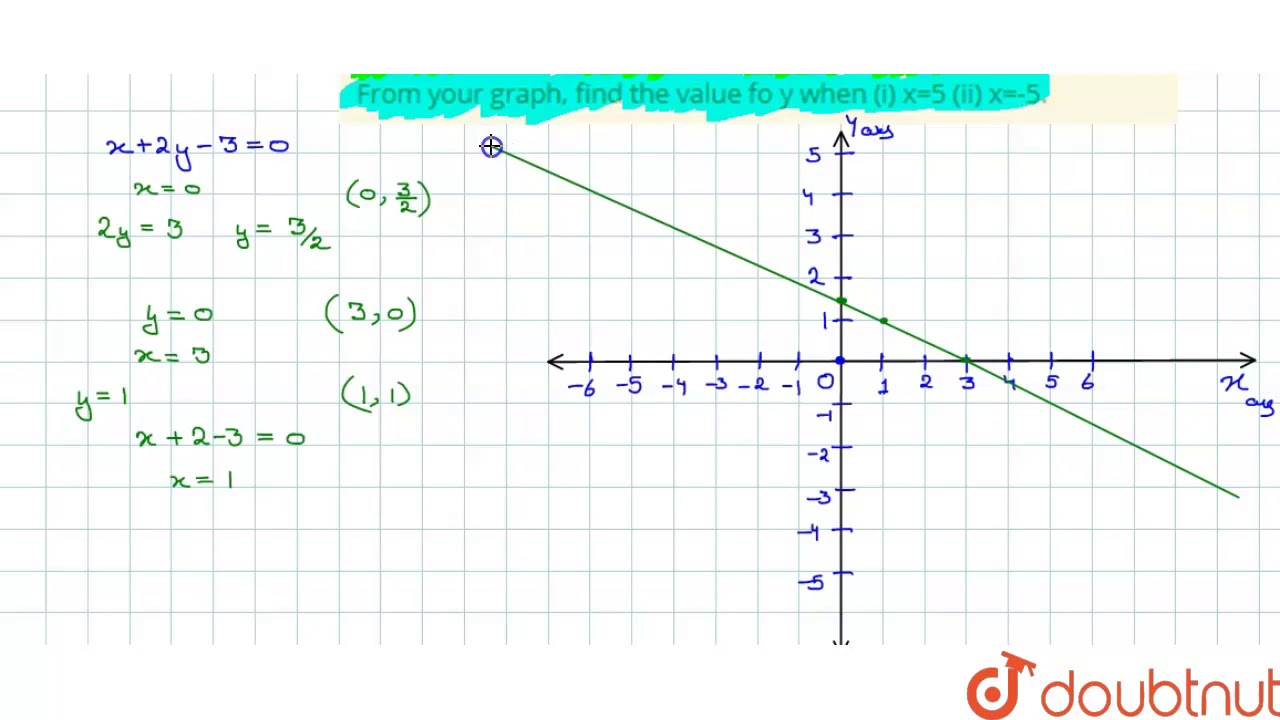
Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube

Graph Graph Equations With Step By Step Math Problem Solver

Linear Relationship Definition

1

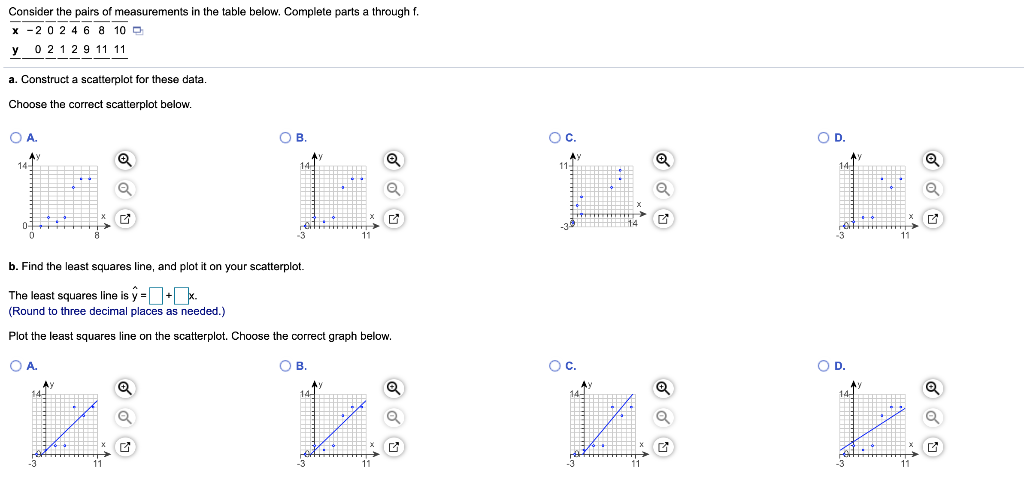
Solved Consider The Pairs Of Measurements In The Table Chegg Com

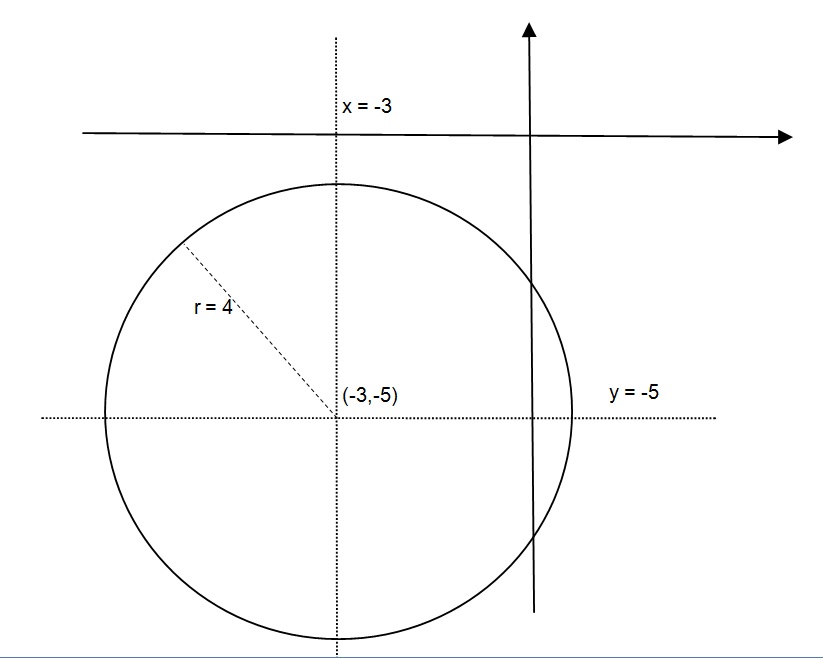
How Do You Graph X 2 4 Y 6 2 9 Socratic

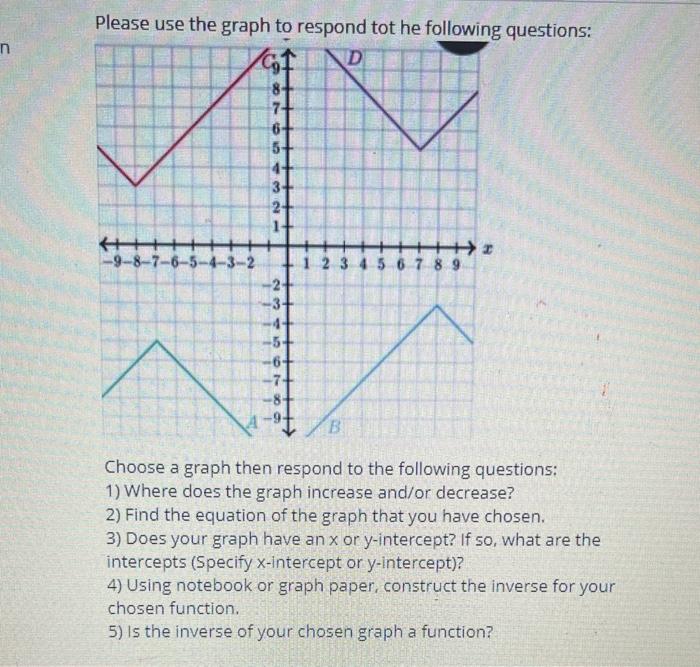
D91f6kyuuj7vjm

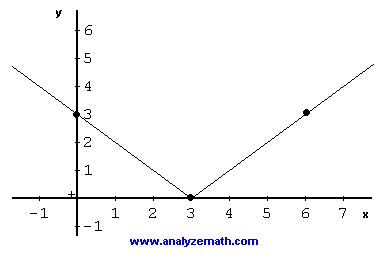
Graphing Square Root Functions

How Do You Graph X 2 Y 2 1 Socratic

Surfaces Part 2

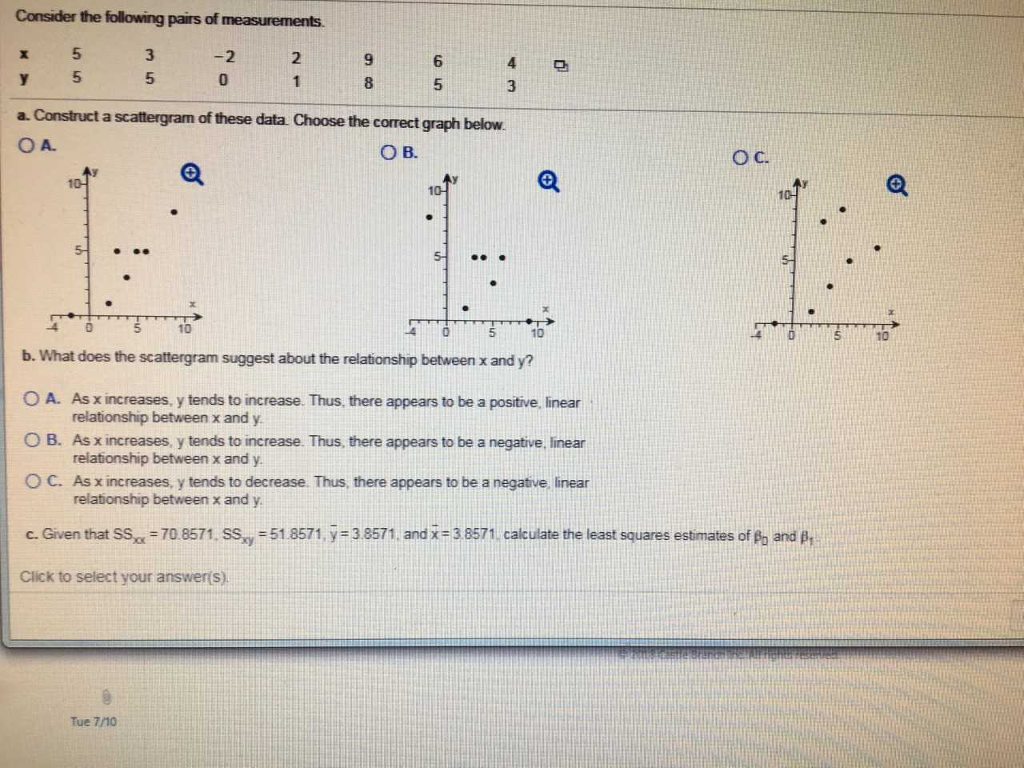
Solved Consider The Following Pairs Of Measurements 5 5 3 2 Chegg Com

What Is The Graph Of X 2 Y 2 Z 2 1 Quora

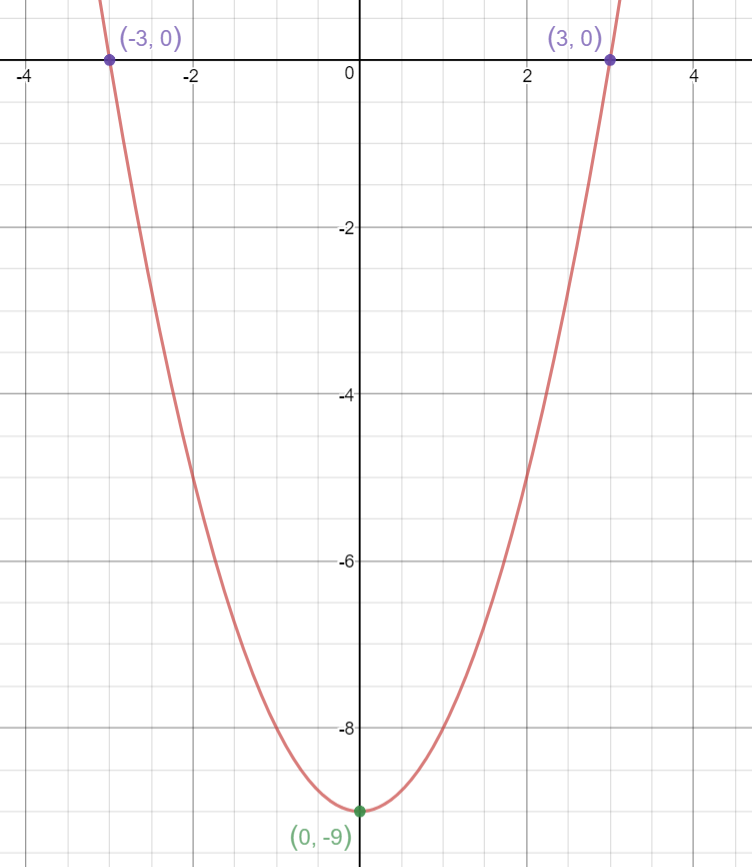
How Do You Graph Y X 2 9 Socratic

Ellipses And Hyperbolae

Graphing Equations Problems 2 Sparknotes

Licensed Electrical Mechanical Engineer Ppt Download

Find The Area Of The Portion Of The Sphere X 2 Y 2 Z 2 25 Inside The Cylinder X 2 Y 2 9 Study Com

2

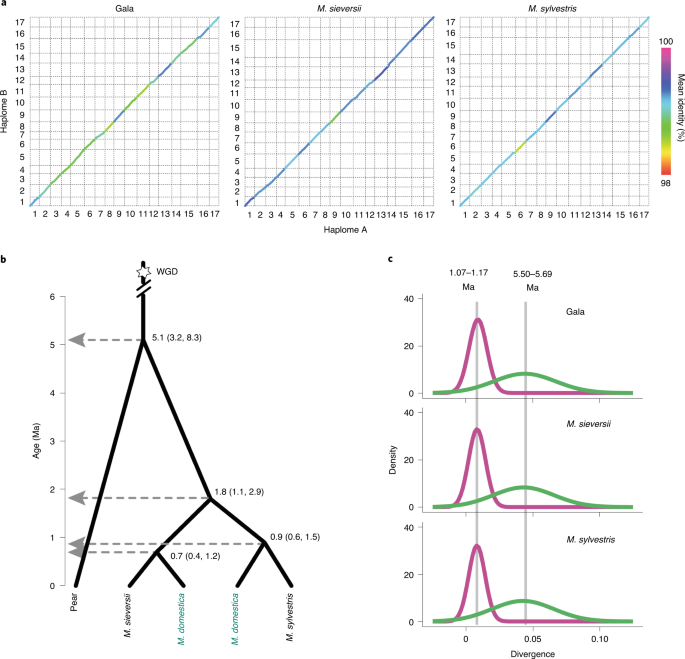
Phased Diploid Genome Assemblies And Pan Genomes Provide Insights Into The Genetic History Of Apple Domestication Nature Genetics

What Is The Graph Of X 2 Y 2 Z 2 1 Quora

Graph X 2 Y 2 4 Youtube

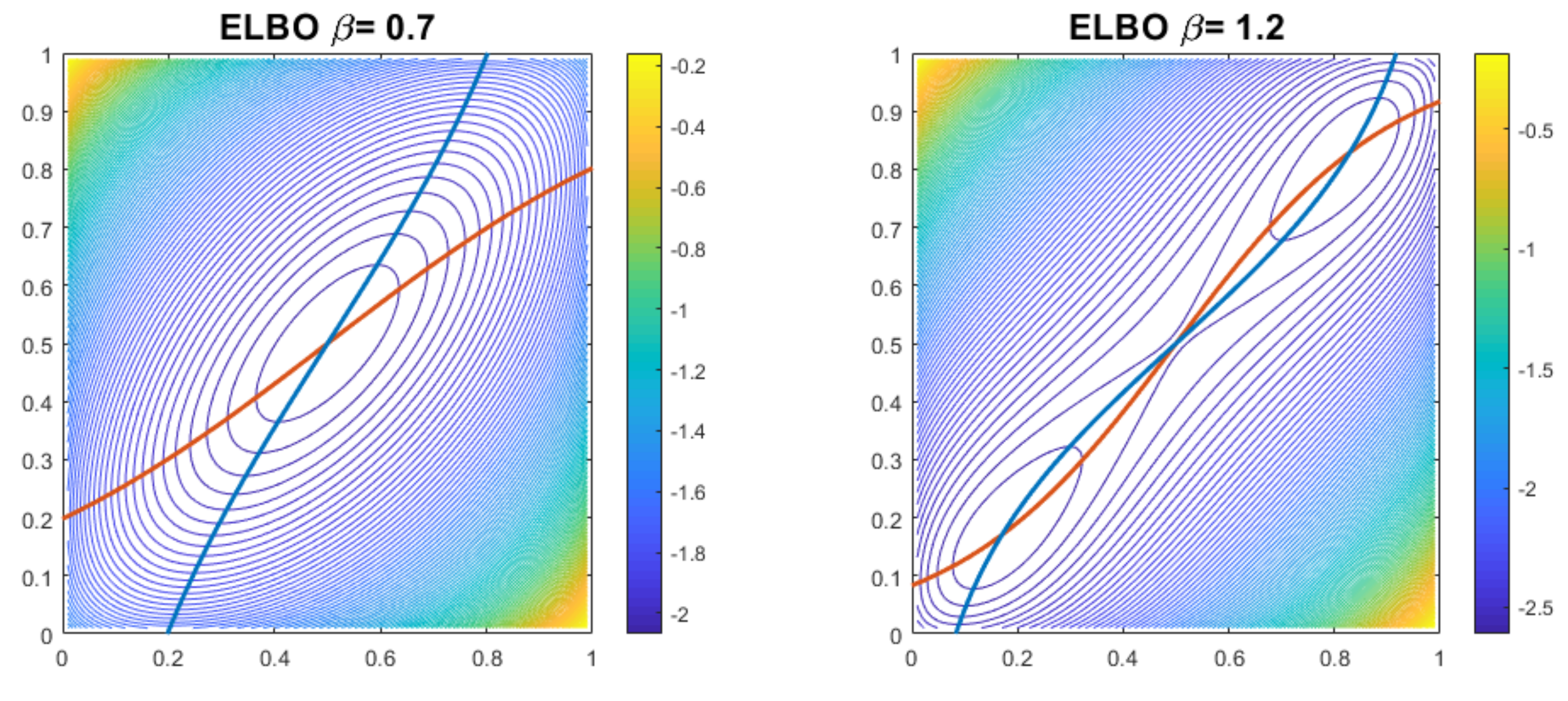
Entropy Free Full Text Dynamics Of Coordinate Ascent Variational Inference A Case Study In 2d Ising Models Html