25 ++ 連立 方程式 グラフ 233073-連立方程式 グラフ 交点
一次関数のグラフの利用１ 無料で使える中学学習プリント
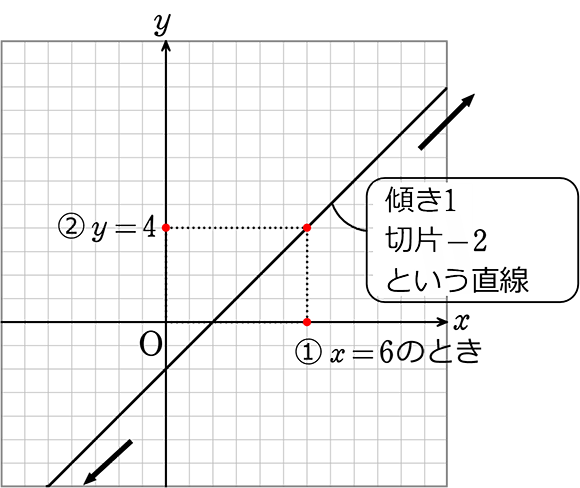
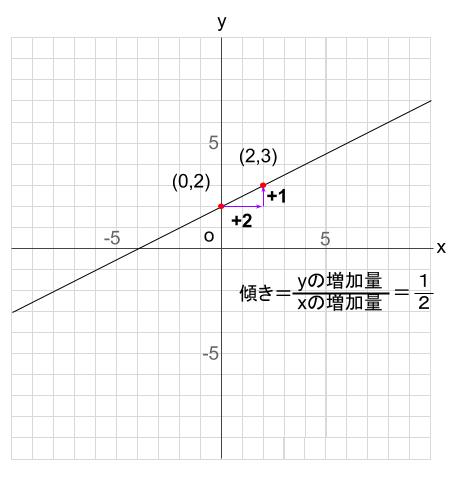
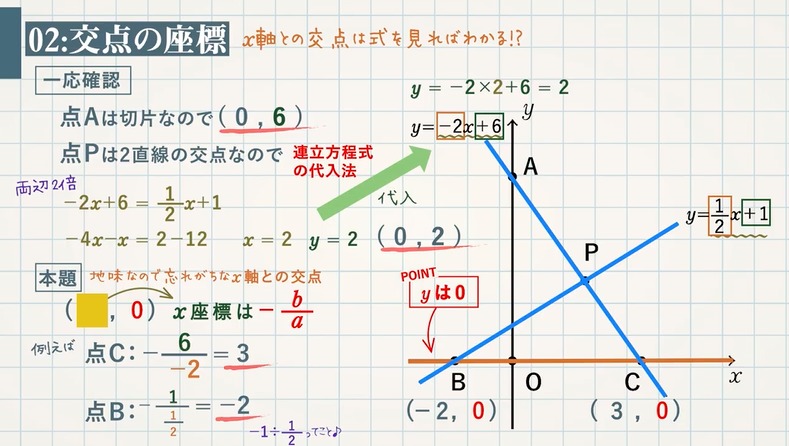
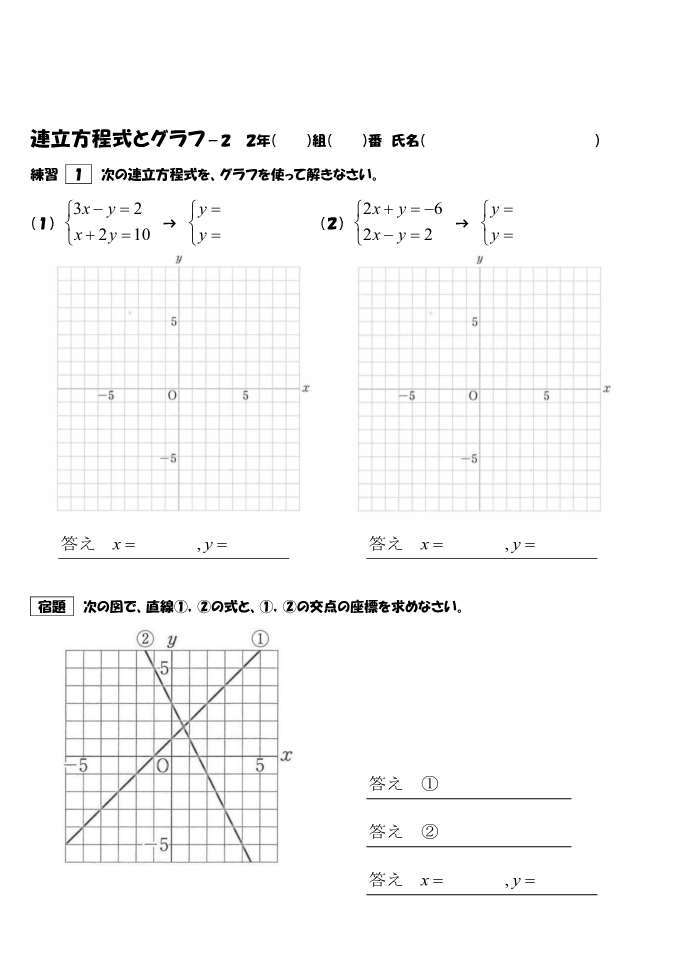
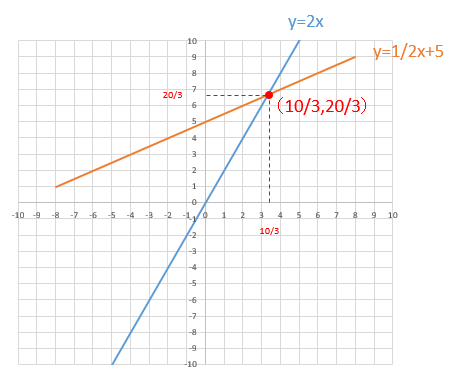
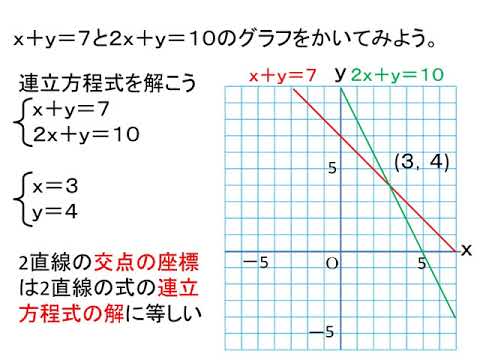
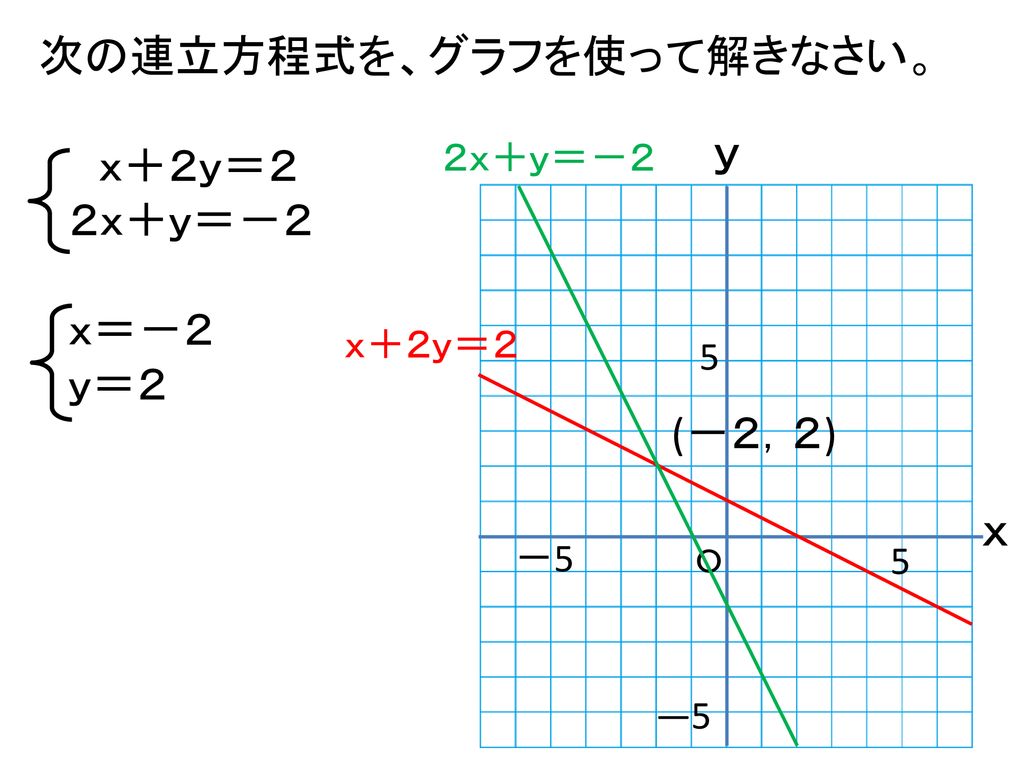
連立方程式の解とグラフ 2元1次方程式のグラフは直線になるので，連立方程式の解 とグラフについては，次のことがいえる。 • それぞれの方程式のグラフの交点のx 座標，y 座標が， 連立方程式の解中学数学～高校入試で出題される 道のり・速さ・時間 を取り扱った 連立方程式の文章題 について、 基礎から難問まで 難易度別&パターン別に解説します。 後半ほど難問です。 家から駅まで2800mの道のりをはじめは分速80mで歩き、途中から分速0mで走っ
連立方程式 グラフ 交点
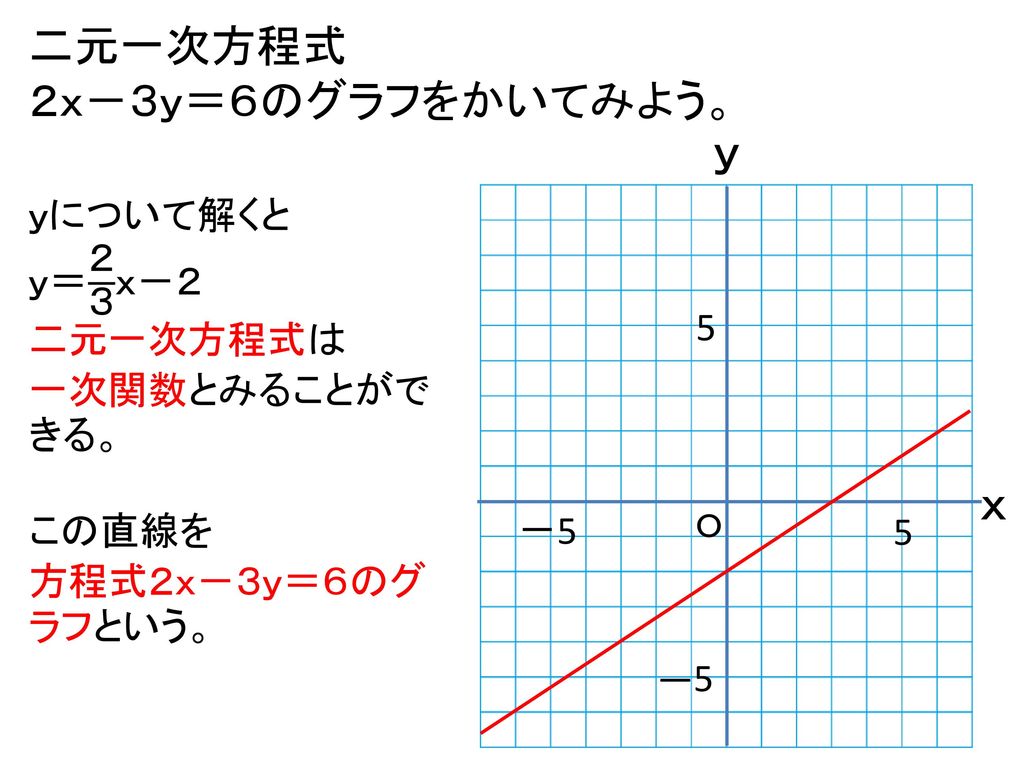
連立方程式 グラフ 交点-連立方程式とは、一般的に といった形で表すことが多い式です。 2元1次方程式と呼ばれる「 2つの変数 (文字) 」と「 最大次数が1 」の式で表されます。 連立方程式の解き方は大きく2つあります。 それは、 加減法 代入法 です。 どちらを用いても連立方程式の解き方①（加減法） 1次関数のグラフの問題 ※1632〜の「グラフ→式を求める」 連立方程式の解き方②（代入法） ※1900〜のところ ※ 垂直二等分線／角の二等分線の図形的な意味 （参考） 2つの式（条件）を満たすのは「交点」ということ
1次関数と2次関数の接点 タカラゼミ
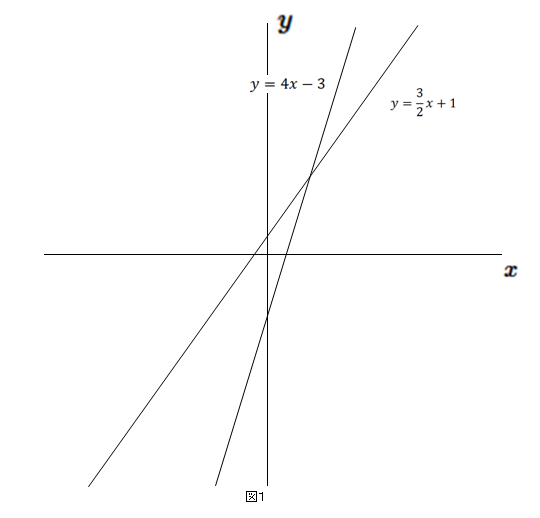
Sway is an easytouse digital storytelling app for creating interactive reports, presentations, personal stories and more Its builtin design engine helps you create professional designs in minutes With Sway, your images, text, videos, and other multimedia all flow together in a way that enhances your story Sway makes sure your creations look great on any screen連立方程式の解は①と②のグラフの交点のχ座標、y座標の組だから χ＝2 答． y＝－2 →52へ 問1 χ＋y＝5 ① 連立方程式 について、 2χ－y＝4② 次の問いに答えなさい。 （1）方程式①、②のグラフをかきなさい。 χ＋y＝5をyについて解くとしかし、これら2つの二元一次方程式を同時に満たす解は、1つしかありません。 それは、x=2 のとき y=5 という解です。 これを簡単に求める方法が「連立方程式」なのです。 今度は、グラフに目を向けます。 y=2x1 のグラフですが、 このグラフ、実は
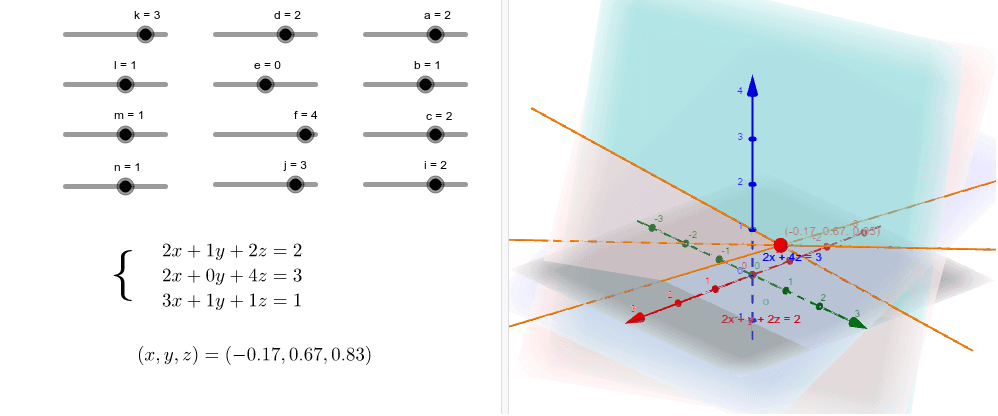
公立高校入試 過去問 英語 教材購入について 「全都道府県 公立高校入試 過去問 数学」単元別の教材購入について ご購入申し込み 購入者特典 お問い合わせ 全都道府県 公立高校入試 過去問 数学 2方程式 2連立方程式（2年） 22 2/01 公立高校入試グラフから読み取れない パターンの問題が多い！！ ①グラフから式を読み取る力 ②連立方程式を使って交点を 求められる計算力 この2つの力が必要！手順 連立方程式を行列で表現し，行列Aと行列Cの係数をExcelシートに入力する． 解が1通り存在するのか確認する．（解が1通り存在することがわかっていれば省略可．） 係数行列Aの逆行列を求める． 求めた逆行列と行列Cの積を求める．これが解．
連立方程式 グラフ 交点のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
3 |  3 | 3 |
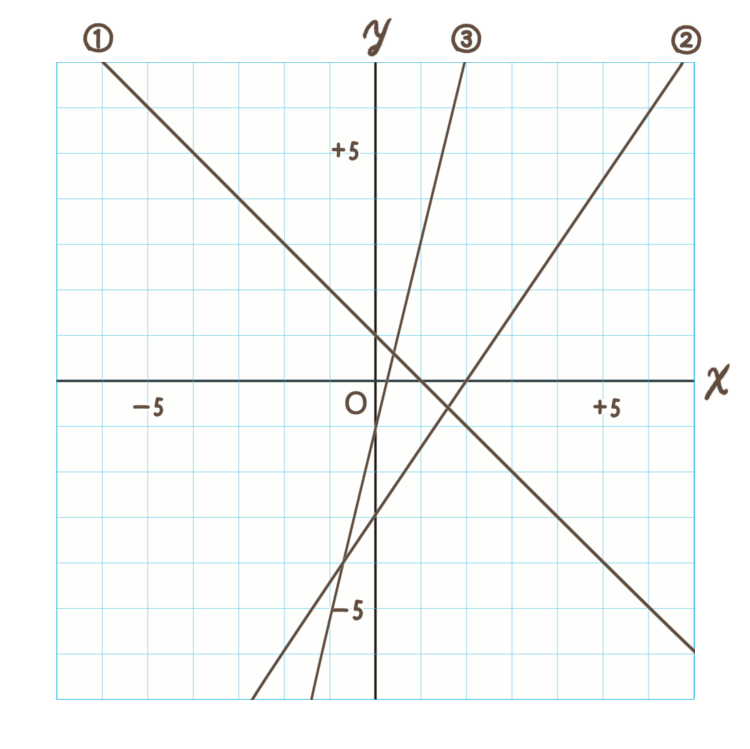
 3 |  3 |  3 |
3 |  3 | 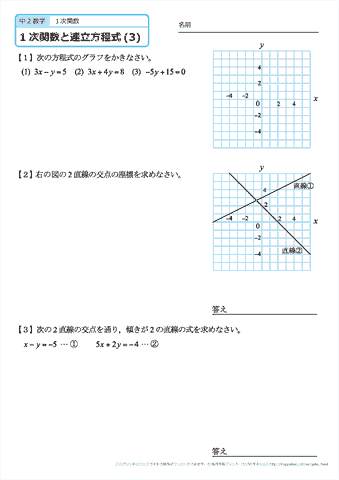 3 |
 3 | 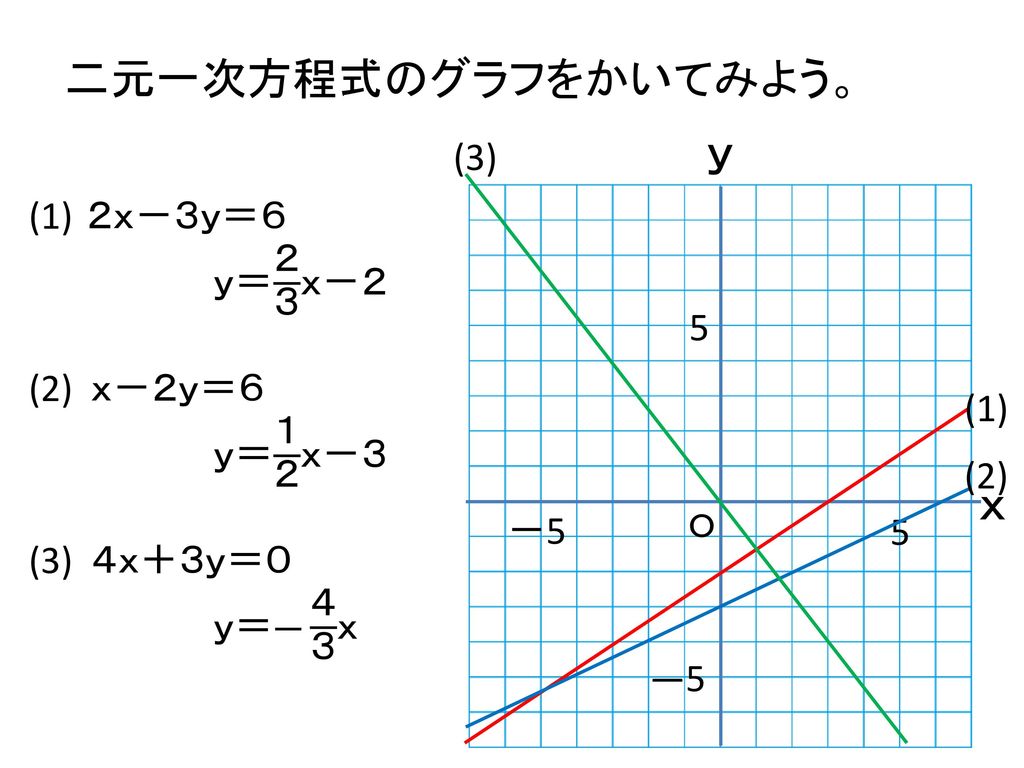3 |  3 |
3 | 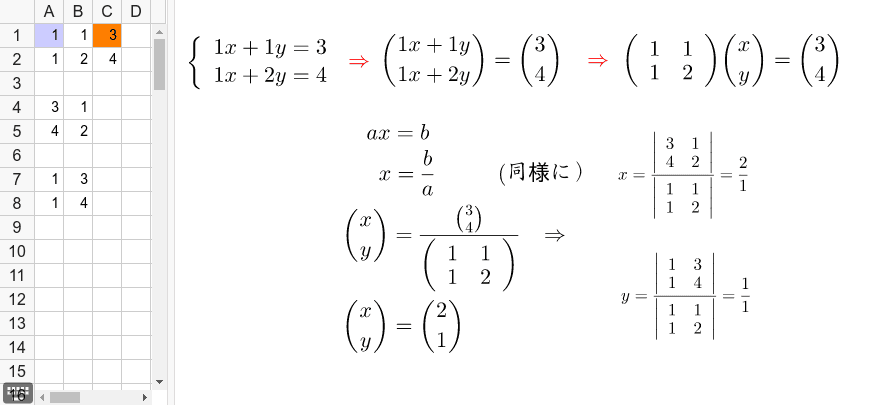3 |  3 |
 3 |  3 |  3 |
3 | 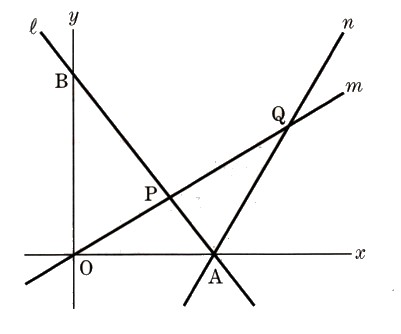 3 |  3 |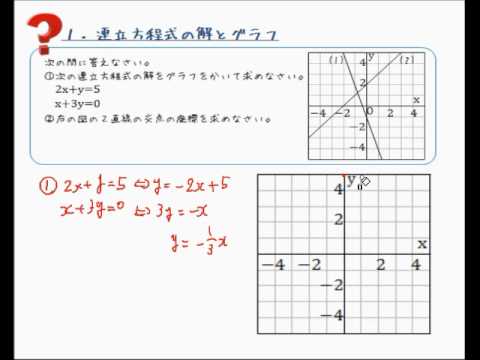
3 | 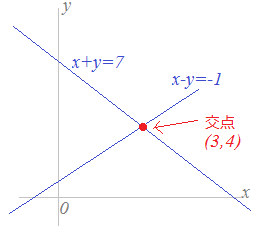 3 |  3 |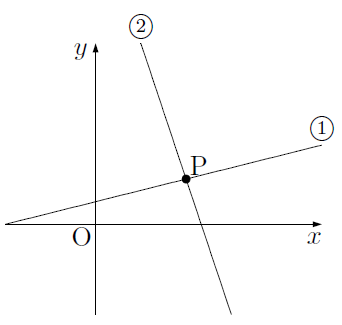
 3 |  3 |  3 |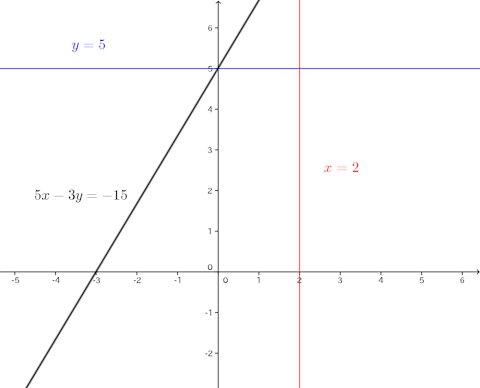
 3 |  3 |  3 |
3 | 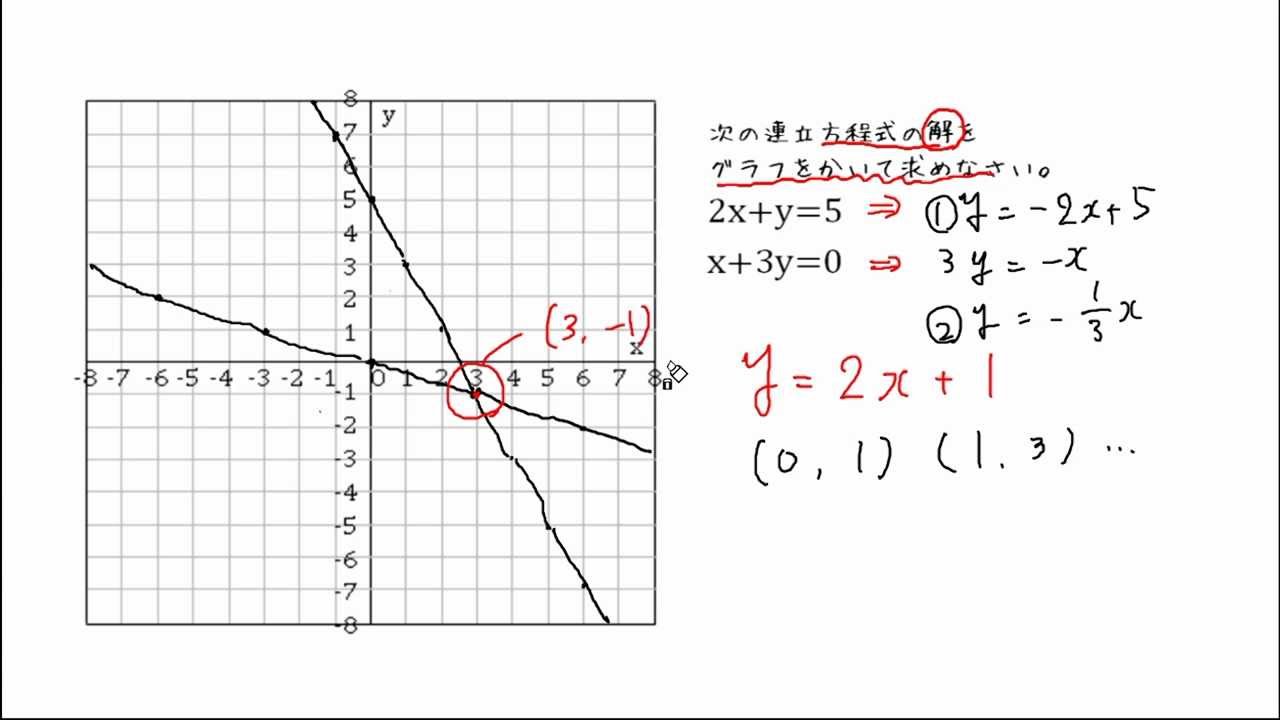 3 |  3 |
 3 | 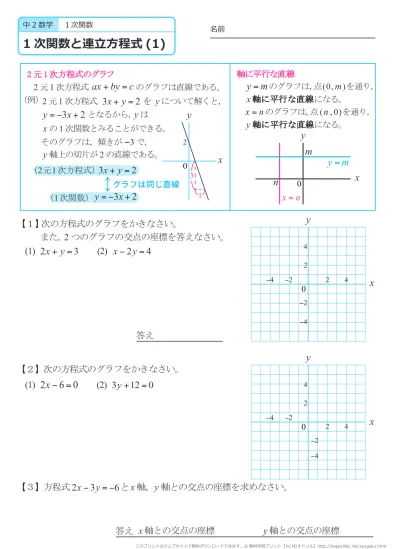 3 | 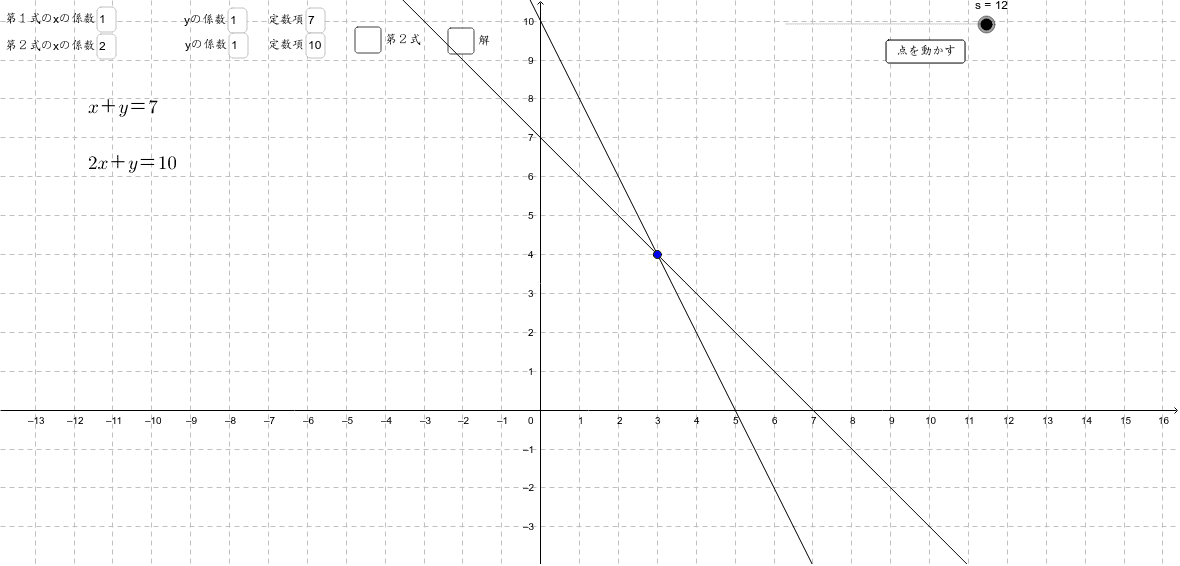 3 |
3 |  3 |  3 |
3 | 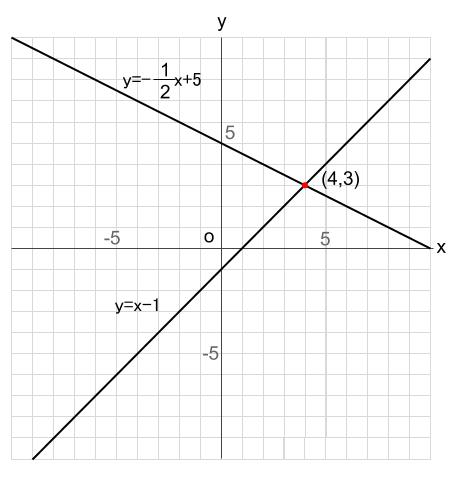 3 | 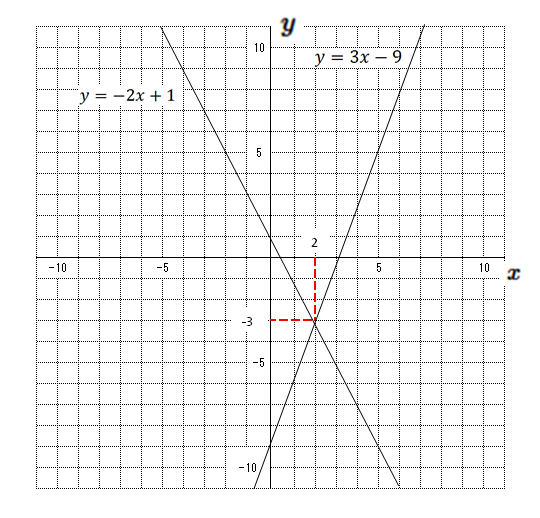 3 |
 3 |  3 |  3 |
3 |  3 |  3 |
3 |  3 | 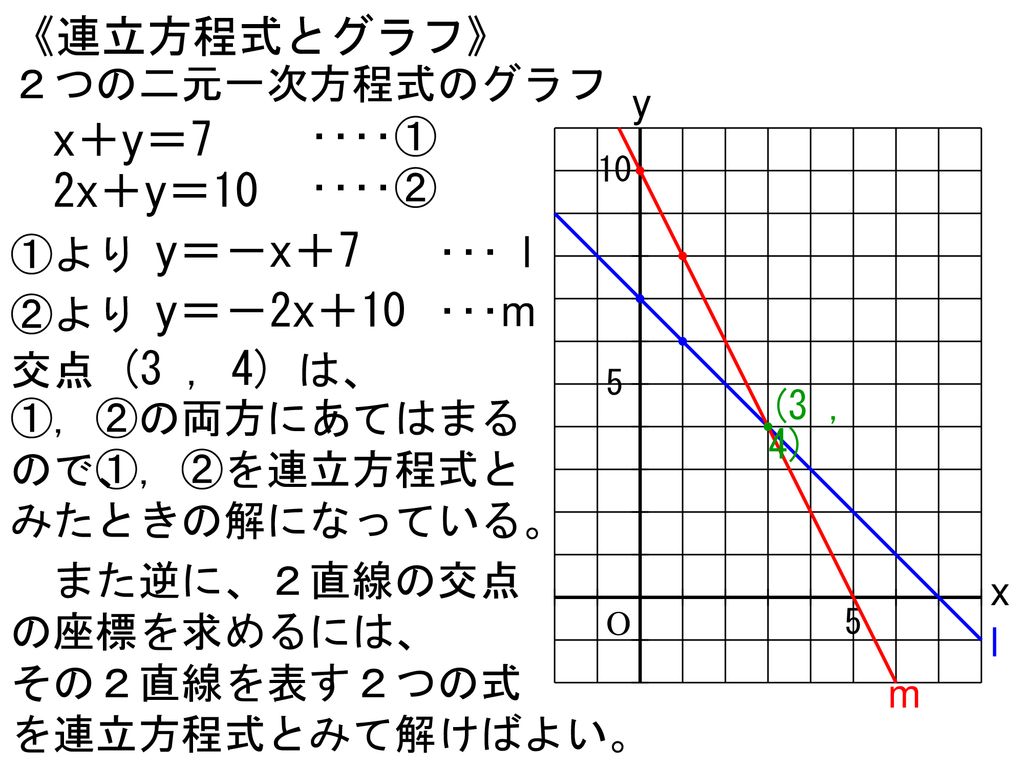 3 |
 3 |  3 | 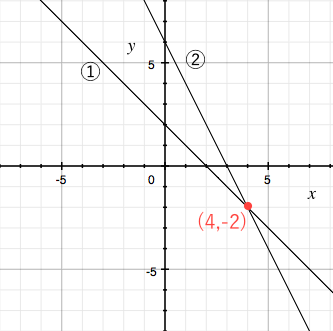 3 |
 3 | 3 |  3 |
 3 | 3 | 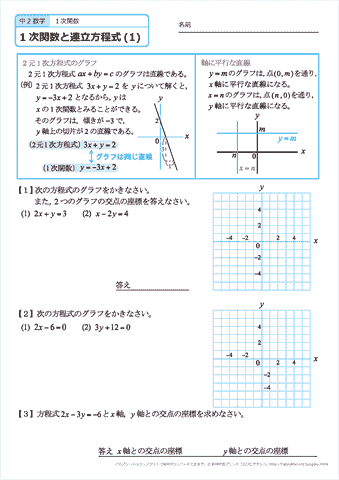 3 |
 3 |  3 | 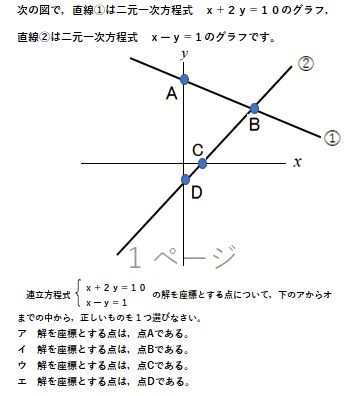 3 |
 3 |  3 |  3 |
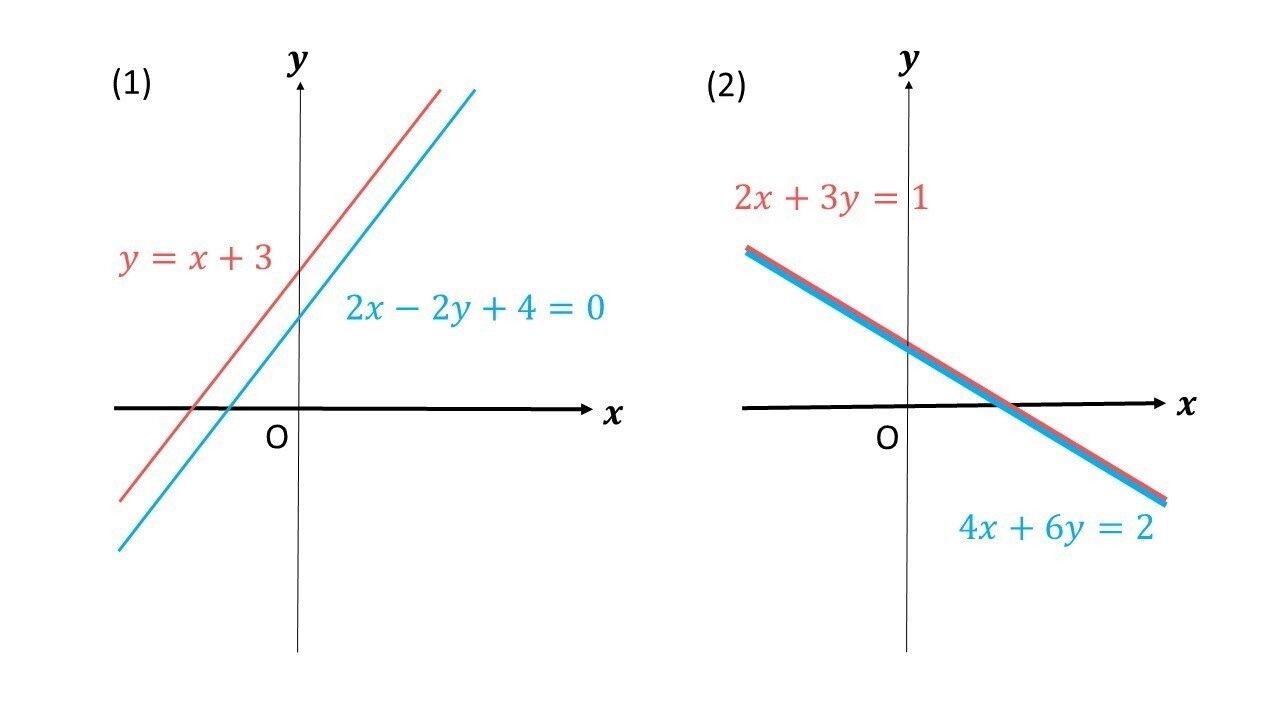 3 | 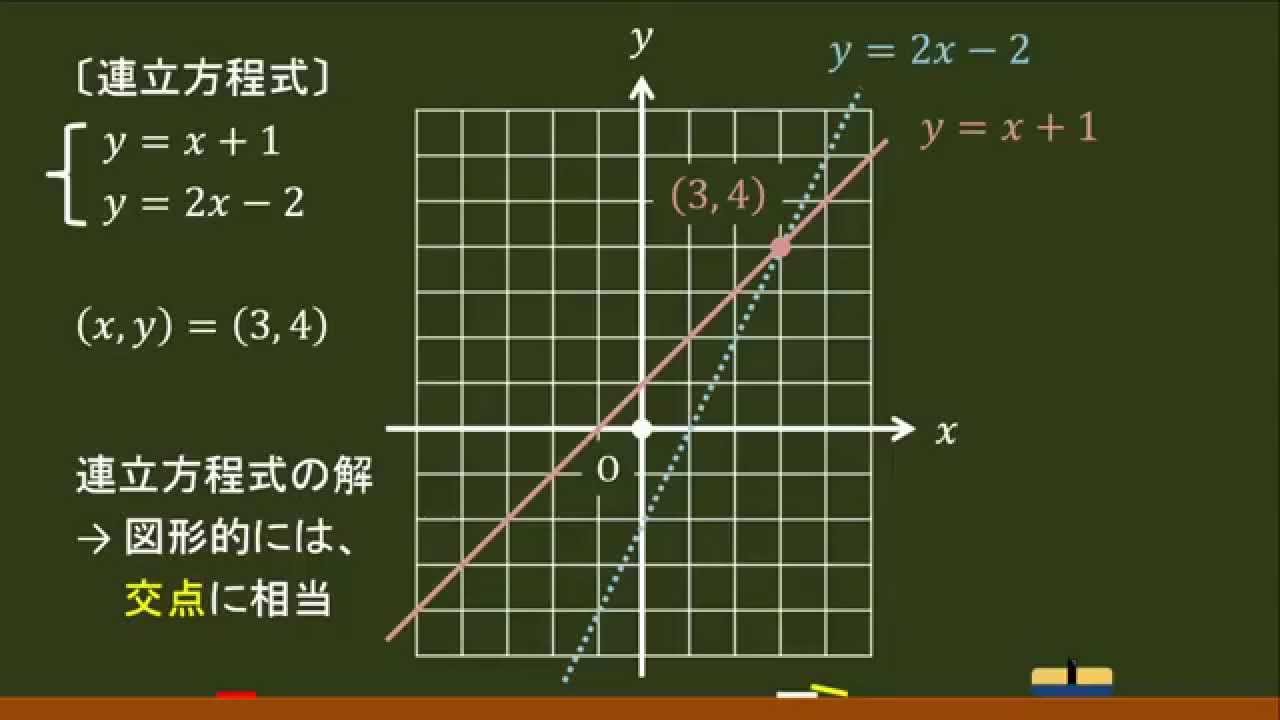 3 | 3 |
 3 |  3 |  3 |
 3 | 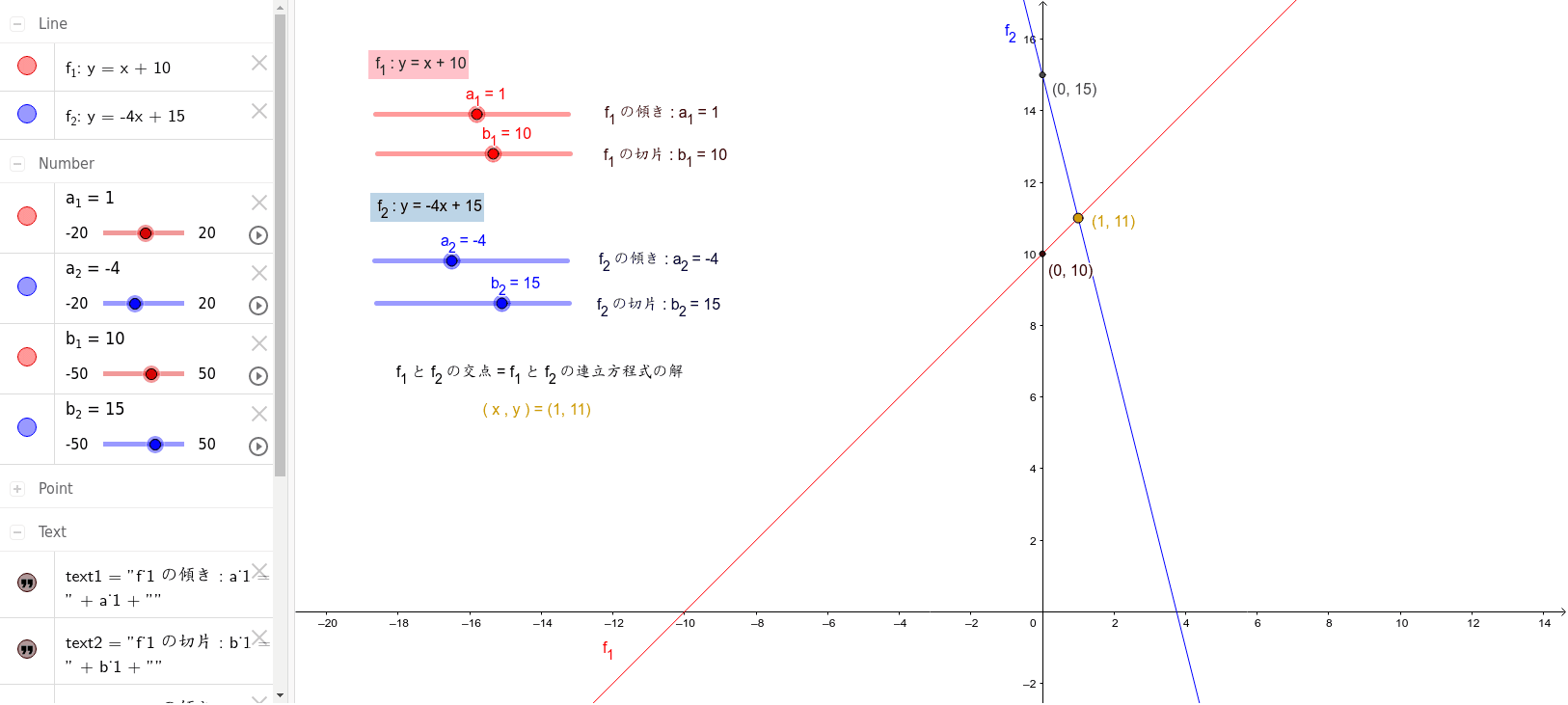 3 |  3 |
 3 |  3 | 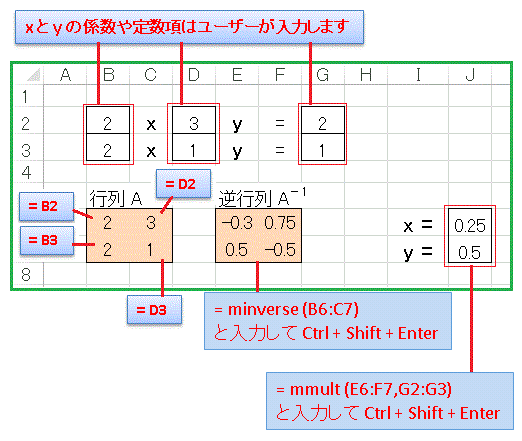 3 |
 3 |  3 | 3 |
 3 | 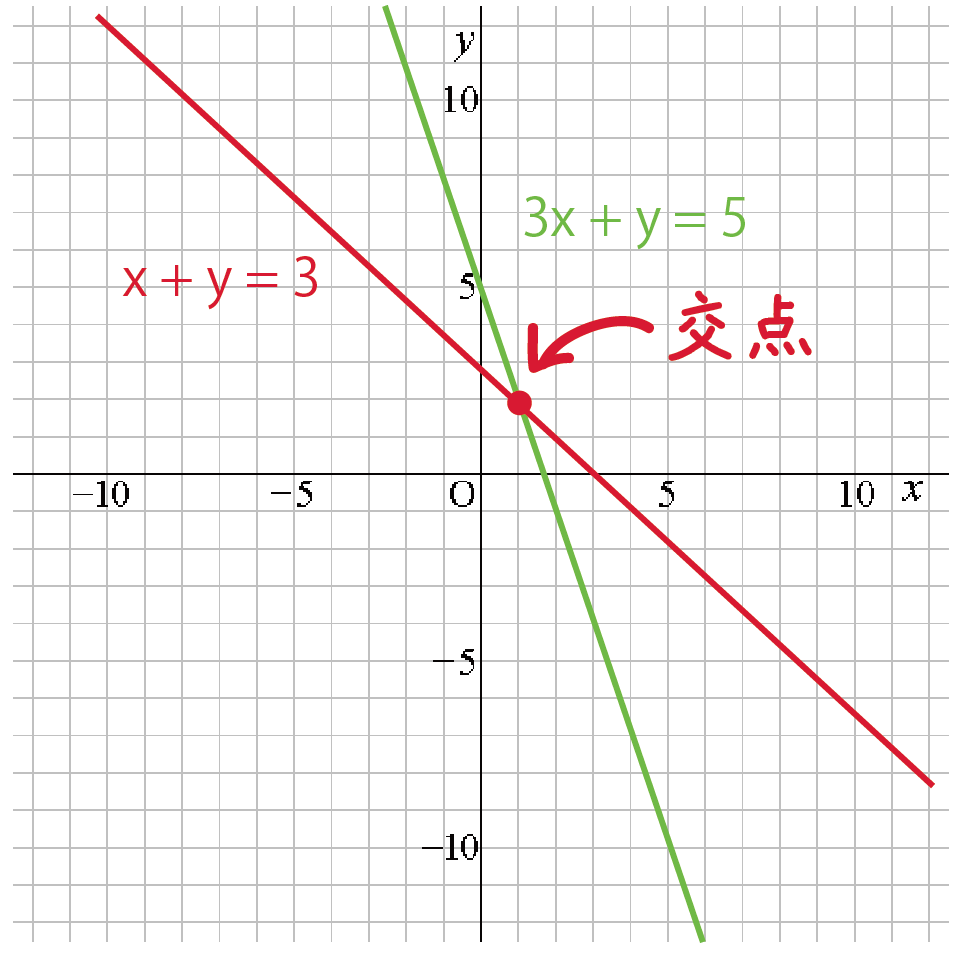 3 |  3 |
 3 | 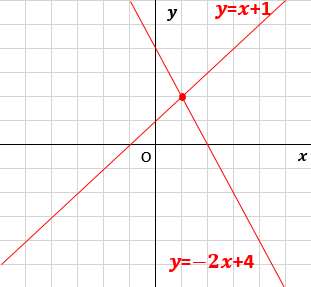 3 | 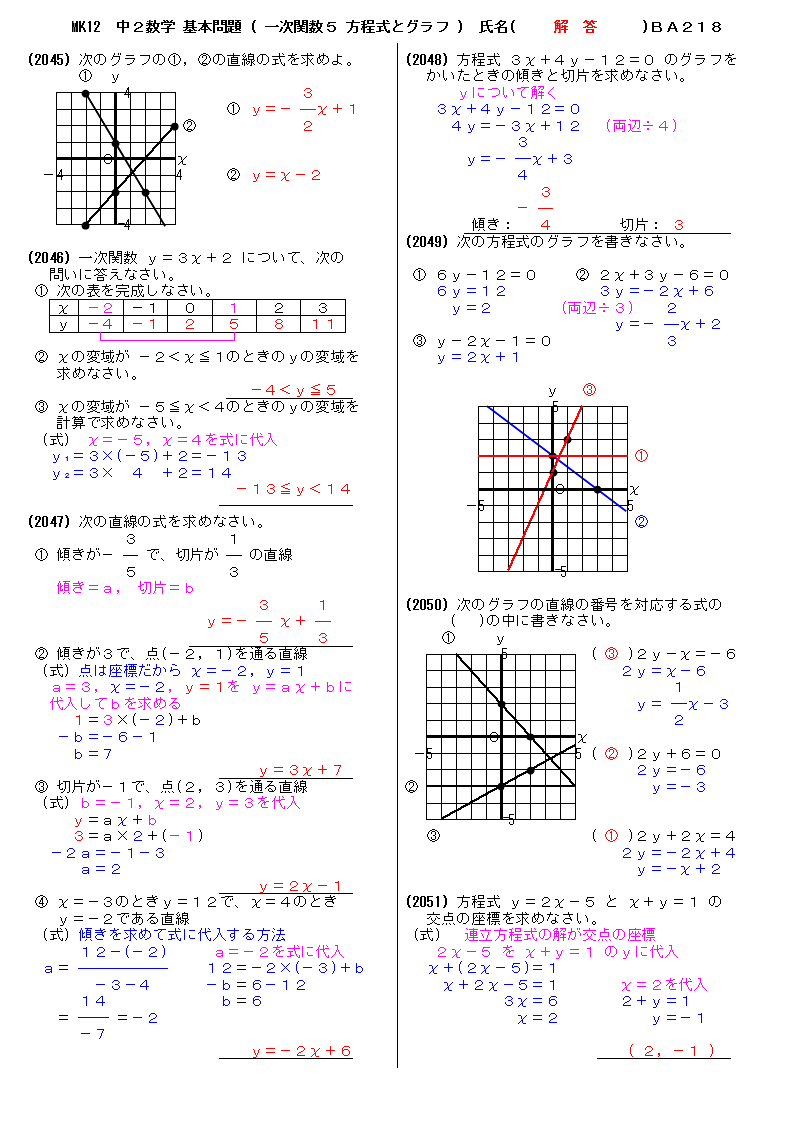 3 |
 3 | 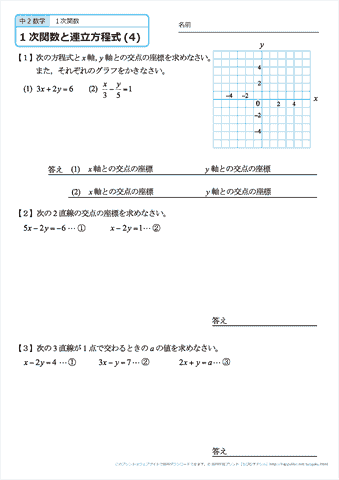 3 |  3 |
 3 |  3 |  3 |
3 |  3 |  3 |
 3 |  3 |  3 |
 3 |  3 | 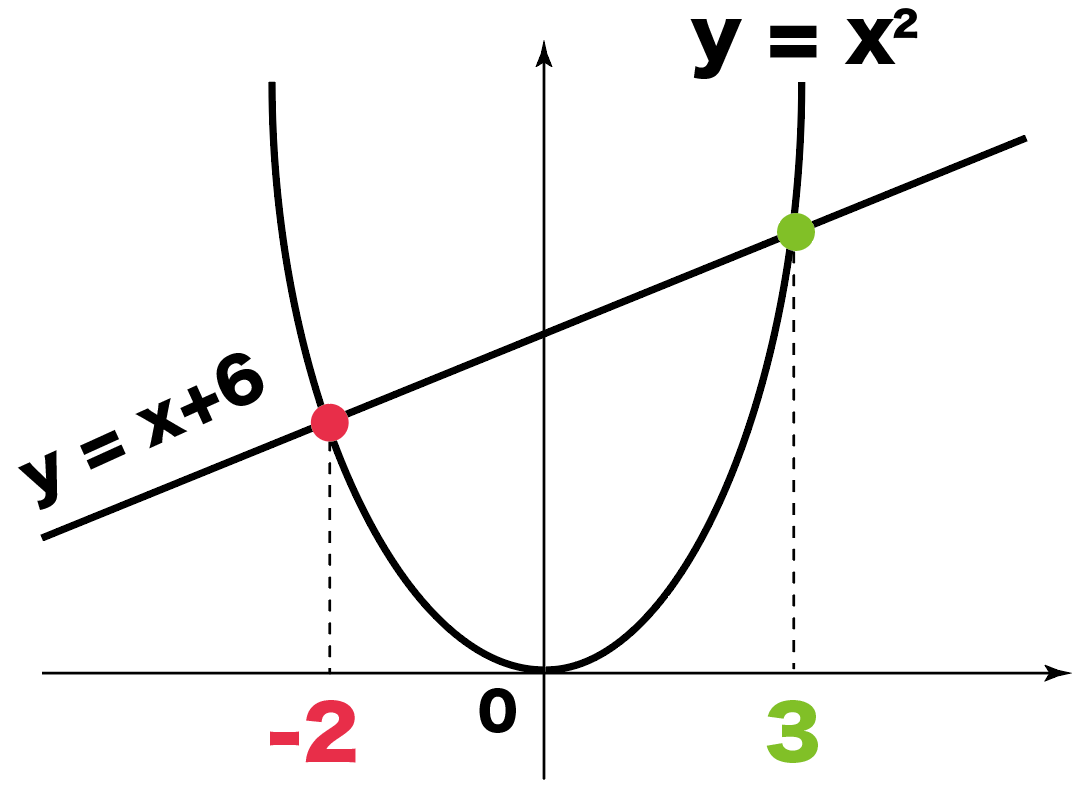 3 |
 3 |  3 |
グラフにおける連立方程式の意味 連立方程式の解 ⇒連立した方程式の共通解 共通解 ⇒グラフの交点 連立方程式の解 ⇒連立した方程式のグラフの交点 「交点」,「交わる」が問題文章中にある ⇒連立方程式を解く可能性 大 重要 6Tips その取扱いをみてみると、実は、スカラー値常微分方程式 → 連立常微分方程式 → 偏微分方程式 という流れでつながることが「後で」分かる．今はまあそういうもうのか、と思ってこの流れについていこう． さて、以前勉強したように、Volterra の被食
Incoming Term: 連立方程式 グラフ, 連立方程式 グラフ 解き方, 連立方程式 グラフ 問題, 連立方程式 グラフ 交点, 連立方程式 グラフ 書き方, 連立方程式 グラフ 分数, 連立方程式 グラフ excel,
コメント
コメントを投稿